1)
x(t)=xo + Vox*t + (ax/2)*t²
x(t)= 0 + 35 * t + (8/2) * t²
xo=0; Vox=35 м/с; ax=8 м/с²
Vx(t)=Vox + ax*t
Vx(t)=35 + 8*t
2)
x(t)=10 - 6*t + (16/2)*t²
xo=10 м; Vox=-6 м/с; ax=16 м/с²
Vx(t)=-6 + 16*t
Тело из точки х=10 м движется против оси координат. Проекция скорости < 0. При этом проекция ускорения >0, значит тело тормозит.
Т.к. ускорение большое, то скоро тело остановится и начнет двигаться вдоль оси координат разгоняясь. Векторы скорости и ускорения будут направлены в одну сторону.
0=-6+16t; 16t=6; t=6/16=3/8 c - время до остановки.
v₀ ≈ = 16,0 м/с; α ≈ 69,6°;
Объяснение:
Дано:
t₁ = 1 c
t₂ = 2 c
v₁ = v₂ = 7.5 м/с
g = 10 м/с²
Найти:
v₀ - начальную скорость
α - угол под которым бросили тело относительно горизонта
Скорость движения тела может быть задана уравнениями
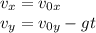
Поскольку траектория движения тела парабола, то наивысшей точки подъёма (вершины параболы) тело достигнет при t₃ = 0.5(t₁ + t₂) = 1.5 c
Вертикальная составляющая скорости тела в этой точке


откуда
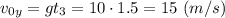
В момент времени t = 1 c

вертикальная составляющая скорости

горизонтальная составляющая скорости

Поскольку горизонтальная составляющая скорости со временем не меняется. то
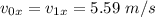
Начальная скорость
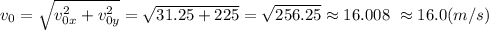
Угол, под которым бросили тело относительно горизонта

Одно деление рычага примем за УСЛОВНУЮ единицу.
Составляем уравнение рычага после сокращения на g получаем:
m₁*3+m₂*1 = m₃*5+m₄*9
8*3+179*1=19*5+m₄*9
m₄*9 = 108
m₄ = 108/9 = 12 кг
Объяснение: