1) x=-2t^2+4t+5
Отсюда мы видим, что график функции зависимости х от времени-парабола, которая ветвями направлена вниз. Отсюда, график пересекает ось ОХ в двух точках. Но в одной точке значение t будет отрицательное, поэтому этот корень отпадает, потому что время не может быть отрицательным. Теперь находим точку когда х=0:
0=2t^2-4t-5
D=16+40=56

x=0 t=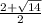
2) Дано- m=0.01кг, h=5м, t=1.2с
Найти - P-?
Решение
h=at^2/2 =>at^2=2h => a=2h/t^2 =>a=10/1.44=6.9 (м/с^2)
строим схему падения тела и получаем уравнение на ось ОУ:
ma=mg-N
N=mg-ma
N=P
P=mg-ma
P=0.01*10-0.01*6.9=0.1-0.069=0.031 (H)
ответ: 0.031 H
МЕСТО БРУСКА КРОЛИК
Объяснение:
Брусок толкнули со скоростью V =10 м/с вверх вдоль доски, наклоненной под углом 30° к горизонту. Обратно он вернулся со скоростью v = 5 м/с. С какой скоростью Vx вернется брусок, если его толкнуть с той же скоростью вдоль той же доски, наклоненной под углом 45° к горизонту.
РЕШЕНИЕ: (пусть масса бруска = m, g = 10 м//с²)
1. Сила трения о доску: F = k*mg*cos30°. k — коэффициент трения.
2. h — высота подъема бруска.
3. S = h/sin30°— длина пути этого подъема.
4. Работа силы трения при полном подъеме:
А = F*S = k*mg*cos30°*h/sin30° = kmgh*ctg30°.
5. Начальная кинетическая энергия ½ mV² при подъеме расходуется так:
½ mV² = mgh + kmgh*ctg30°. (*)
6. При спуске имеем: mgh = kmgh*ctg30° + ½ mv² (**)
7. Вычитаем (**) из (*), получаем:
½ mV² – mgh = mgh – ½ mv², откуда:
2mgh = ½ mV² + ½ mv².
8. Сократив массу, имеем: h = (50 + 12,5)/20 = 3,13 м.
9. Из (*) получаем (подставив скорость и высоту): k = (50 – 31,3)/(31,3*ctg30°) = 0,345.
10.Теперь для угла 45° вместо (*) имеем: ½ mV² = mgh + kmgh*ctg45° (***), откуда, зная k и ctg45° = 1, получим:
½ V² = gh’ + kgh’*1 ==> h = 50/(10 + 3,45) = 3,71 м.
11.И теперь из (**) — с учетом угла 45° получим:
gh’ = kgh’*1 + ½ (Vx)²:
(Vx)² = 2(37,1 – 0.345*37.1) = 48,6, откуда:
Vx = 6.97 = ~7 м/с.