Длина бруска: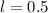 
м.
Ширина бруска: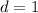 
м.
Высота бруска: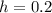 
м.
Плотность морской воды: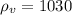 
кг/м³.
Найти нужно разницу веса в воде и на суше: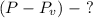 
1. Найдём объём бруска: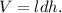 
2. Масса вычисляется по формуле: 
.
3. Вес тела на суше найти довольно просто, по 3-му закону Ньютона, он по модулю равняется силе тяжести: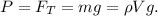 
4. На тело в воде действует две силы - сила тяжести и сила Архимеда. Вес будет равняться их разности: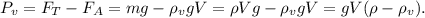 
5. Найдём заданную в условии разность: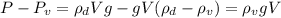 
.
6. Перепишем (4) с учётом (1):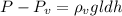 
.
Численно: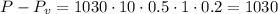 
(Н).
_________________________________________
> Задача #3Дано:Объём вытесненной ртути: 
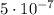см³ = 
м³.
Плотность стекла: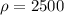 
кг/м³.
Найти нужно вес пробирки в воздухе: 
1. Из закона Архимеда следует, что объём вытесненной жидкости равен объёму погруженной части тела, то есть: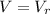 
.
2. Масса вычисляется по формуле: .
3. Вес пробирки в воздухе: 
.
Численно: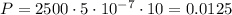 
(Н).
Переведём в милиньютоны: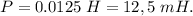 
1) Если тело за равные промежутки времени проходит разные пути, то его движение называют неравномерным.
2) Обычно движение с возрастающей по модулю скоростью называют ускоренным движением.
3) Движение же с убывающей скоростью - замедленным движением.
4) Равноускоренное прямолинейное движение - это движение с постоянным по модулю ускорением, при котором векторы скорости и ускорения параллельны.
5) Равнозамедленное прямолинейное движение - это движение с постоянным по модулю ускорением, при котором векторы скорости и ускорения направлены противоположно.
6) Ускорение — физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени. Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.
7) Да, формула для скорости при равноускоренном движении: v=v0+at v = v 0 + a t . Здесь v0 - начальная скорость тела, a=const a = c o n s t - ускорение. Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии.
8)Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду [м/с²], [m/s²]. Также могут применяться и производные величины от скорости и от времени.