

Объяснение:
Данный тип задач решается следующим образом:
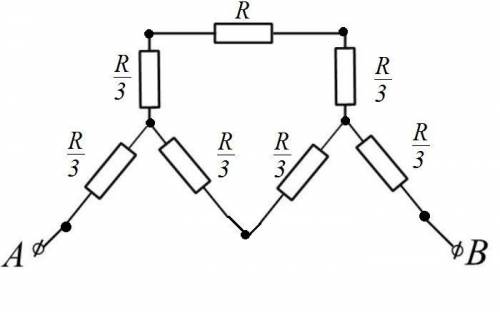
Левый и правый "треугольники" заменяем соединениями в "звезду".
(См. получившуюся схему).
Сопротивление первой, верхней ветви:
R₁ = R/3 + R + R/3 = 5·R / 3
Сопротивление параллельной ей ветви:
R₂ = R/3 + R/3 = 2·R / 3
Далее находим сопротивление этих двух ветвей:
R₁₂ = R₁·R₂ / (R₁+R₂) = 10·R / 21
И, наконец, общее сопротивление цепи:
Rобщ = R/3 + 10·R/21 + R/3 = 8·R/7
Учтем, что R = 35 Ом, получаем:
R общ = 8·35 / 7 = 40 Ом.
Решение задачи упростил тот факт, что сопротивления исходной цепи были одинаковыми.
Ве́кторная величина — физическая величина, являющаяся вектором (тензором ранга 1). Противопоставляется с одной стороны скалярным (тензорам ранга 0), с другой — тензорным величинам (строго говоря — тензорам ранга 2 и более). Также может противопоставляться тем или иным объектам совершенно другой математической природы. В большинстве случаев термин вектор употребляется в физике для обозначения вектора в так называемом «физическом пространстве», то есть в обычном трёхмерном пространстве классической.
Если что-то неправильно значит ошибка в условии.
Объяснение:
Цель работы: Определить кол-во теплоты, отданное горячей водой и полученное холодной при теплообмене, и объяснить полученный результат.
Приборы и материалы: Калориметр, мензурка, термометр
Ход работы:
1. Измерить температуру холодной воды (25 градусов)
2. Узнать массу холодной воды (100 г.)
3. Перелить холодную воду в калориметр.
4. Измерить температуру горячей воды (78 градусов)
5. Перелить горячую воду в калориметр.
6. Измерить температуру смеси (37 градусов)
Рабочая формула
Q=cm(t1-t2)
c = 4200 Дж
m1 = 100 г.
m2 = 100 г.
t1 = 25 градусов
t2 = 78 градусов
Q1=4200*100*(37-78)= -17220 Дж
Q2=4200*100*(37-25)=5040 Дж
Результаты переписать в таблицу.
Вывод: Q=Q1. Q>Q1 это связано с тем, что всегда имеет место не только теплообмен между двумя порциями воды в калориметре, но и с окружающей средой.