5 с
Объяснение:
Запишем уравнение движения Фокса и Форда, приняв для последнего начальную координату за x₀₂ и скорость за v₂:
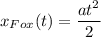
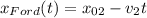
Тогда, расстояние между ними подчиняется закону:
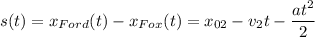
По условию, в некоторый момент времени τ это расстояние удовлетворяет условию:
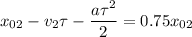
Скорости Фокса и Форда:
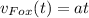
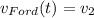
Их относительная скорость в момент времени τ:
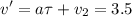 м/с
м/с
Подставляя все исходные данные в уравнения получим систему:
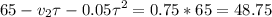
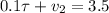
Выражаем скорость Форда из второго уравнения и подставляем ее в в первое:
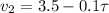
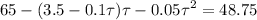
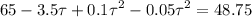
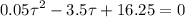
Решая полученное квадратное уравнение, находим два корня 65 и 5 секунд. Скорости Форда, соответствующие этим временам 3,5-0,1*5=3 м/с и 3,5-0,1*65=-3 м/с, значит нам подходит решение 5 секунд, так как для 65 секунд Форд идет не на встречу Фоксу, а убегает от него.
p = 760 мм. рт. ст. 760·133,3 ≈ 1·10⁵ Па
<Vкв> = 400 м/с
ρ - ?
1)
Запишем формулу среднеквадратичной скорости:
<Vкв> = √ ( 3·R·T/M)
Возведем ее в квадрат:
<Vкв>² =3·R·T/M
Отсюда:
R·T = M·<Vкв>²/3 (1)
2)
Запишем уравнение Менделеева-Клапейрона:
p·V = m·R·T / M
Разделим на объем:
p = (m/V)·R·T / M
Учтем, что плотность ρ = m/V
p = ρ·R·T / M
Отсюда:
R·T = p·M / ρ (2)
3)
Приравняем (1) и (2):
M·<Vкв>²/3 = p·M / ρ
Отсюда:
ρ = 3·p·/ <Vкв>² (M - сократили).
Подставляем:
ρ = 3·p·/ <Vкв>² = 3·1·10⁵ / 400² ≈ 1, 9 кг/м³