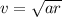 , где a - модуль вектора центростремительного ускорения тела, видно, что скорость прямо пропорциональна расстоянию от центра окружности, по которой движется тело (каждая точка будет двигаться тем быстрее, чем дальше она находится от центра вращения), поэтому на корабле качка будет усиливаться по мере приближения к носу.
, где a - модуль вектора центростремительного ускорения тела, видно, что скорость прямо пропорциональна расстоянию от центра окружности, по которой движется тело (каждая точка будет двигаться тем быстрее, чем дальше она находится от центра вращения), поэтому на корабле качка будет усиливаться по мере приближения к носу.
54 км/ч
Объяснение:
(120 + 150) / (2 + 3) = 270/5 = 54 км/ч