Пояснение к рисункам:
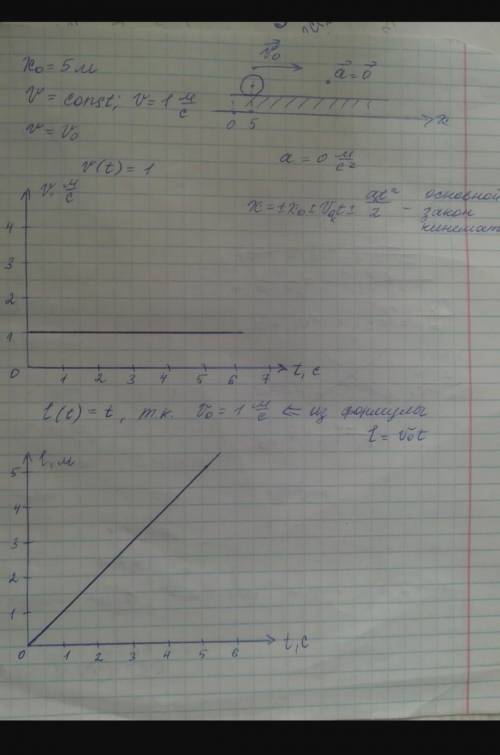
Нарисуем физический рисунок и обозначим на нем известные величины. В условии сказано, что тело движется со скоростью 1 м/с, т. е. скорость тела не изменяется, значит, V=const, V0=V. Тело движется вдоль оси ОХ, и движется сонаправленно. Начальная координата тела - 5 м, я спроецировала её на ось ОХ. Делаем вывод о том, что движение равномерное и прямолинейное.
При прямолинейном движении ускорение равно 0 м/с^2.
Основной закон кинематики:
x=±x0±V0x*t±axt^2/2
Воспользуемся им.
1. V(t). Скорость при прямолинейном равномерном движении, как было сказано ранее, константа, поэтому график имеет вид прямой и параллелен оси Оt.
2. l(t). Из основного закона кинематики: S=V0t+at^2/2, а в данном случае S=l.
Из формулы l=V0t (а=0 м/с^2, поэтому опускаем второе слагаемое) после подстановки значения V0 (а это у нас 1 м/с) имеем функцию l=1t.
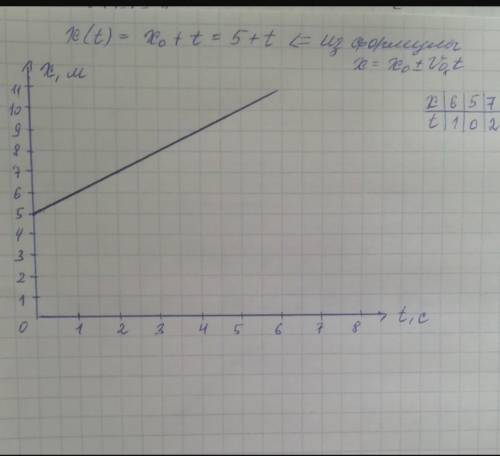
3. x(t). Пользуемся основным законом кинематики, подставляем известные значения x0, V0 и получаем функцию вида x=5+t.
сила тяжести груза mg=60нmg=60н значительно больше силы, с которой надо тянуть веревку, чтобы удержать груз. это определяется существенными силами трения веревки о бревно. сначала силы трения препятствуют соскальзыванию груза под действием силы тяжести. полный расчет распределения сил трения, действующих на веревку, довольно сложен, поскольку сила натяжения веревки в местах ее соприкосновения с бревном меняется от f1f1 до mgmg. в свою очередь сила давления веревки на бревно также меняется, будучи пропорциональной в каждой точке соответствующей локальной силе натяжения веревки. соответственно и силы трения, действующие на веревку, определяются именно указанными силами давления. однако для решения достаточно заметить, что полная сила трения fтрfтр (слагающие которой пропорциональны в каждой точке силе реакции бревна) будет с соответствующими коэффициентами пропорциональна силам натяжения веревки на концах; в частности, с некоторым коэффициентом kk она будет равна большей силе натяжения: fтр=kmgfтр=kmg. это означает, что отношение большей силы натяжения к меньшей есть величина постоянная для данного расположения веревки и бревна: mg/t1=1/(1−k)mg/t1=1/(1−k), поскольку t1=mg−kmgt1=mg−kmg. когда мы хотим поднять груз, концы веревки как бы меняются местами. сила трения теперь направлена против силы t2t2 и уже не , а мешает. отношение большей силы натяжения, равной теперь t2t2, к меньшей - mgmg будет, очевидно, таким же, как и в первом случае: t2/mg=1/(1−k)=mg/t1t2/mg=1/(1−k)=mg/t1. отсюда находим, что t2=(mg)2/t1=90н источник:
1. 2,27кДж
2. 26кДж
3. 35кДж