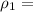 =13,6 г/см^3=13600 кг/м^3 (плотность ртути)
=13,6 г/см^3=13600 кг/м^3 (плотность ртути)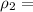 =1000 кг/м^3 (плотность воды)
=1000 кг/м^3 (плотность воды)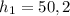 см=0,52 м
см=0,52 м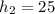 см=0,25 м
см=0,25 м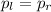 (1)
(1)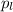 - давление столба жидкости расположенного над "контрольным" уровнем в левом колене.
- давление столба жидкости расположенного над "контрольным" уровнем в левом колене.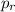 - давление столба жидкости расположенного над "контрольным" уровнем в правом колене.
- давление столба жидкости расположенного над "контрольным" уровнем в правом колене.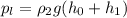 (2)
(2)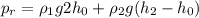 (3)
(3)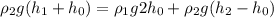
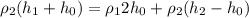
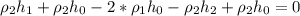

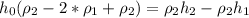
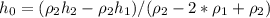
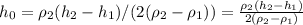 (5)
(5)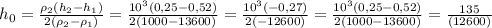 ≈0,0107 м=1,07см=10,7мм
≈0,0107 м=1,07см=10,7мм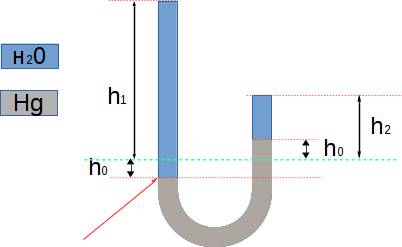
Объяснение:
1. Дано:
m = 600 кг
α = 20°
F - ?
Согласно первому и второму закону Ньютона
( При v = const ( следовательно а = 0 м/с² ) )
F - mgsinα = 0 ( Докажите самостоятельно )
F = 600 * 10 * sin20° ≈ 2050 Н
2. Дано:
m = 10 кг
а = 2,5 м/с²
Р - ?
Согласно второму закону Ньютона
ma = N - mg
Где N - сила реакции опоры
N = m( g + a )
Но P = | N | , При N > 0 Н
Р = m( g + a )
P = 10( 10 + 2,5 ) = 125 Н
3. Дано:
h = 40 м
L = 400 м
μ = 0,05
v - ?
Согласно ЗСЭ
mgh = ( mv² )/2 + Aтр.
mgh = ( mv² )/2 + Fтр.L
mgh = ( mv² )/2 + μNL
Согласно первому и второму закону Ньютона
N - mgcosα = 0 ( Докажите самостоятельно )
Где α - угол наклона наклонной плоскости ( относительно горизонта )
Отсюда
N = mgcosα
mgh = ( mv² )/2 + μmgcosαL
При v << c следовательно m = const
gh = v²/2 + μgcosαL | * 2
2gh = v² + 2μgcosαL
v = √( 2gh - 2μgcosαL )
v = √( 2g( h - μcosαL ) )
Согласно теореме Пифагора и базовым понятием тригонометрии
cosα = √( L² - h² )/L ( Докажите самостоятельно )
Тогда
v = √( 2g( h - ( μL√( L² - h² ) )/L ) )
v = √( 2g( h - μ√( L² - h² ) ) )
v = √( 2 * 10( 40 - 0,05√( 400² - 40² ) ) ) ≈ 20 м/с
4. Дано:
m = 50 кг
R = 4 м
v = 6 м/с
P - ?
Согласно второму закону Ньютона
При прохождении среднего положения равновесия ( низшей точки траектории )
maцс. = mg - N
N = m( aцс. + g )
При aцс. = v²/R
N = m( v²/R + g )
Р = | N | , Т.к. N > 0 Н
Р = m( v²/R + g )
Р = 50( 6²/4 + 10 ) = 950 Н