 секунд от начала отсчёта времени – нос электрички уже был высунут за пределы моста на эти самые несколько десятков метров. Т.е. понятно, что нос электрички достиг окончания моста МЕНЕЕ ЧЕМ ЗА
секунд от начала отсчёта времени – нос электрички уже был высунут за пределы моста на эти самые несколько десятков метров. Т.е. понятно, что нос электрички достиг окончания моста МЕНЕЕ ЧЕМ ЗА 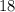 секунд!
секунд!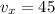 км/ч .
км/ч .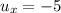 км/ч .
км/ч .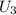 равна алгебраической сумме проекций
равна алгебраической сумме проекций 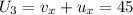 км/ч
км/ч 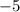 км/ч
км/ч 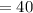 км/ч .
км/ч . секунд
секунд 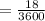 часа
часа 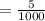 часа
часа 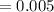 часа, студент относительно земли переместился точно на длину моста. Найдём длину моста
часа, студент относительно земли переместился точно на длину моста. Найдём длину моста 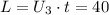 км/час
км/час 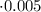 часа
часа 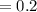 км
км 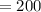 м .
м .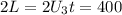 м .
м .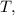 в течение которого ВСЯ электричка проезжала по мосту, разделим путь, который она проделала за это время на её скорость:
в течение которого ВСЯ электричка проезжала по мосту, разделим путь, который она проделала за это время на её скорость: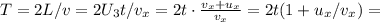
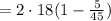 сек
сек 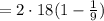 сек
сек 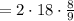 сек
сек 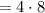 сек
сек 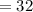 сек .
сек .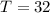 сек .
сек .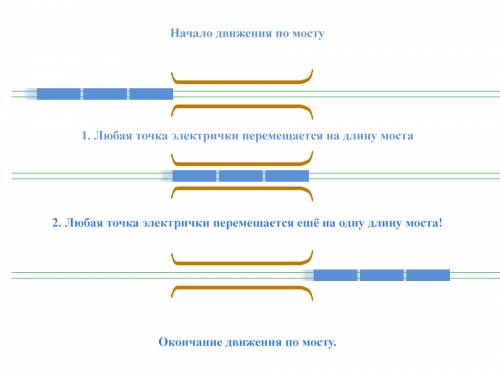
погружение кубика в воде k = 0,8 объема
плотность воды p1 = 1000 кг/м3
плотность кубика p2
долита жидкость с плотностью р3
высота слоя жидкости h = 8 см и совпадает с верхней гранью кубика
закон архимеда для кубика плавающего в воде гласит что масса кубика равна массе вытесненой воды
S*H*p2=S*(H*k)*p1
значит р2 = k*p1
закон архимеда для кубика плавающего в смеси двух жидкостей гласит что масса кубика равна массе вытесненых жидкостей
S*H*p2=S*(H-h)*p1+S*h*p3
значит H*p2=(H-h)*p1+h*p3
p3 = (H*p2-(H-h)*p1)/h =
= (H*k*p1-(H-h)*p1)/h =
= p1*(H*k-(H-h))/h =
= p1*(1-H/h*(1-k)) = 1000*(1-9/8*(1-0,8)) кг/м3 = 775 кг/м3 - это ответ
p3 = p1*(1-H/h*(1-k)) - общая формула для этой и аналогичных задач