Объяснение:
В начале движения тело имеет кинетическую энергию, которая с набором высоты превращается в потенциальную. На максимальной высоте кинетическая энергия у тела равна 0, так как скорость равна 0.
Кинетическая энергия - mv²/2, где m - масса тела, v - скорость в конкретной точке
Потенциальная энергия - mgh, где m - масса тела, g - ускорение свободного падения, h - высота нахождения тела
а) Так как кинетическая энергия перейдет в потенциальную, можно записать:
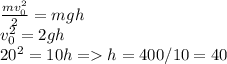 м
м
б) m*20²/2=200m дж - кинетическая энергия в начальной точке
200m/5 =40m дж - уменьшенная кинетическая энергия
В каждой точке справедливо равенство:
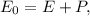 где E0 - начальная кинетическая энергия, E и Р - кинетическая и потенциальная энергии в конкретной точке
где E0 - начальная кинетическая энергия, E и Р - кинетическая и потенциальная энергии в конкретной точке
P=200m-40m=160m - потенциальная энергия в точке, в которой кинетическая уменьшилась в 5 раз
160m=10mh
h=160/10=16 м - искомая высота
в) Используя данные и выражения предыдущего пункта, получим:
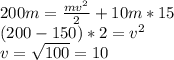 м/с
м/с
Объяснение:
Ця формула для визначення періоду коливань математичного маятника була виведена і перевірена на дослідах голландським фізиком К. Гюйгенсом (1629 — 1695), тому її часто називають формулою Гюйгенса.
Період коливань математичного маятника залежить лише від прискорення вільного падіння в даному місці Землі і від довжини маятника. Період не залежить від амплітуди коливань і від маси підвішеного тягарця, що легко перевірити на дослідах з різними маятниками. Слід лише пам'ятати, що розміри тягарця мають бути малими порівняно з довжиною підвісу і що малим має бути також кут відхилення маятника від вертикалі. З наведеної залежності періоду коливань математичного маятника можна легко експериментально визначити прискорення вільного падіння. Для цього треба виміряти довжину маятника і період його коливань.
я незнаю
Объяснение:
такое ищо не учмла