Легкая задача.
Дано:
M=0,032кг/моль.
V=700м/с^2;
R=8,31 Дж/(моль*К).
T=?
Для начала, разберемся с формулой, нам известна формула средней квадратичной скорости молекулы. Формула имеет вид:
v2cp=(3*k*T)/m0
Формула (1).
Т.к. k=R/Na, а m0=M/Na. (Нам нужны эти преобразования, чтобы упростить формулу, и перейти к нашему условию).
Подставим эти формулы в (1)
v^2(cp)=(3*R*T/Na)*(Na/M);
Получаем:
v^2(cp)=3*R*T/M;
Все данные нам известны, подставляем данные:
v^2(cp)*M=3*R*T;
T=v^2(cp)*M/3*R;
T=490000*0,032/3*8,31=628,96=629К.
Либо, переводя в градусы, получаем:
T=629-273=356 градусов Цельсия.
ответ: 1.4м/c 1м/c 1м/c 0м/c
Объяснение:
Мгновенный центр вращения квадрата располагается на перпендикуляре к скорости v, а значит лежит на прямой AD. Известно, что угловая скорость вращения ω =4 рад/c. Чтобы найти скорость v, нужно умножить расстояние от центра вращения на угловую скорость вращения. Определим расстояние от центра вращения:
x =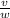 
= 0.25м
Заметим, что это расстояние в точности равно стороне квадрата. Известно, что скорость v направлена к точке В, а также, что направление обхода вершин квадрата совпадает с направлением его вращения. Это значит, что из двух точек лежащих на прямой AD, нам подходит только точка D => точка D является мгновенным центром вращения и ее скорость равна 0.
Теперь легко определяем скорости точек C и B:
Vc = ωa = 1м/c
Vb = ω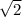
a = 1.4 м/c
m= E/gh = 400 : 80 × 10 = 0,5.