Найдем формулу, связывающую амплитудное значение тока в контуре с амплитудным значением напряжения. Как известно напряжение в контуре
U(t)=q(t)C=>qmax=Umax∗C(1) В тоже время I(t)=dqdt=q′(t). Величина заряда меняется по гармоническому закону q(t)=qmaxcos(ωt)=>I(t)=q′(t)=−qmax∗ωsin(ωt), таким образом мы получили, что Imax=−qmaxω(2) подставляем (1) в (2) Imax=−UmaxCωОсталось найти циклическую частоту ω=2πT, в то же время период равен по формуле Томсона T=2πLC−−−√, подставляем в (2)Imax=−Umax∗C2πT=−Umax∗C2π2πLC−−−√==−Umax∗CLC−−−√=−UmaxCL−−√Подставляем данные задачи Imax=−500В400∗10−12Ф10∗10−3Гн−−−−−−−−−−−√=−0,1А
1) пройденный путь расчитывается по формуле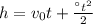
. Тут нам неизвестно а,которое мы можем вычислить из формулы второго закона ньютона а=F/m, а так же неизвестно время движения,которое мы можем вывести из формулы скорости тела.Ускорение будет равно a=8Н/0,4 кг=20 м/с в кв. формула для расчета времени будет выглядеть вот так 
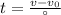. Предварительно переведя все в систему Си посчитаем время. начальная скорость будет равна нулю т.к. тело изначально покоилось получим t=23.9 м/с/20 м/с в кв=1,2 с. Подставим это время и ускорение в формулу пройденного пути и получим h=(20*1,44)/2=14,4 м