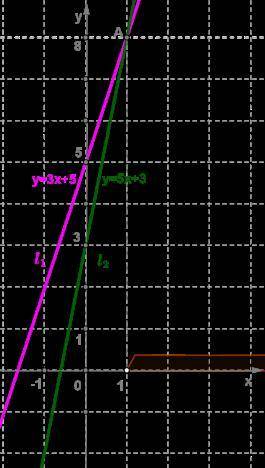
Для решения неравенства 3x+5<5x+3 построим графики линейных функций, расположенных в правой и левой части данного уравнения, т. е. построим графики y=3x+5 и y=5x+3.
Для построения графика каждой линейной функции составим таблицу значений.
Для функции y=3x+5 имеем:
x 0 1
y 5 8
Через полученные точки проведём прямую l1.
Для функции y=5x+3 имеем:
x 0 −1
y 3 −2
Через полученные точки проведём прямую l2.
Прямые y=3x+5 и y=5x+3 пересекаются в точке A(1;8). В этой точке значения функций равны.
Используя построение, делаем вывод: для того чтобы значение первой функции было меньше значения второй функции, необходимо, чтобы первый график был ниже второго, т. е. при x>1.
Можно проверить ответ, полученный при построении, решая неравенство:
3x+5<5x+3;3x−5x<3−5;−2x<−2;x>1.
Объяснение:
Дано:
Масса троллейбуса: m = 12 × 10³ кг.
Время движения: t = 5 c.
Пройденный путь: S = 10 м.
Коэффициент трения: μ = 0,02.
Ускорение свободного падения: g = 10 м/с².
Найти нужно силу тяги: Fт — ?
1. Запишем уравнение зависимости пути от времени: а так как , то
2. Выразим ускорение из (1):
3. Распишем силы действующие на тело по оси Oy:
4. Распишем силы действующие на тело по оси Ox:
5. Сила трения по определению и с учётом (3):
6. Выразим силу тяги из (4):
7. Объединяем формулы (2), (5) и (6):
Численно получим:
(H).
Переведём в кН для удобства: 12000 Н = 12 кН.
ответ: 12 кН.
Объяснение:
Поставь 5 звезд и сделай лучшим позязя)