Груз массой 250 г совершает колебания на пружине жесткостью 0.8 кн/м.найти период,собственную циклическую частоту механических колебаний.

👇

Ответ:

Milana8211

22.07.2020

Дано:
m = 250 г = 0,250 кг
k = 0,8 кН/м = 800 Н/м

T -?
ω - ?
Циклическая частота:
ω=√ (k/m) = √ (800 / 0,250) ≈ 56,6 рад/с

Период:
T = 2*π/ω = 2*3,14 / 56,6 ≈ 0,11 c

4,7(99 оценок)

Открыть все ответы

Ответ:

Ангелина0611

22.07.2020

1). Все представленные графики соответствуют графикам равноускоренного движения (за равные промежутки времени скорость для каждого графика возрастает (убывает) на одну и ту же величину).

Для тела с графиком движения 5:

Движение тела прямолинейное равноускоренное, так как скорость тела с течением времени равномерно возрастает.

Ускорение на графике скорости равноускоренного движения численно равно тангенсу угла наклона графика к оси времени:

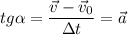
$\displaystyle tg\alpha=\frac{\vec v-\vec v_{0}}{\Delta t}=\vec a$

Учитывая по вертикали 1 кл = 1 м/с и по горизонтали 1 кл = 1 с:

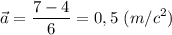
$\displaystyle \vec a=\frac{7-4}{6}=0,5 \ (m/c^{2})$

Скорость тела через 10 с после начала отсчета времени:

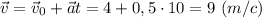
$\displaystyle \vec v=\vec v_{0}+\vec at=4+0,5\cdot10=9 \ (m/c)$

Перемещение тела за 10 с после начала отсчета времени:

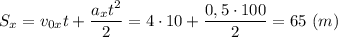
$\displaystyle S_{x}=v_{0x}t+\frac{a_{x}t^{2}}{2}=4\cdot10+\frac{0,5\cdot100}{2}=65 \ (m)$

Так как движение тела прямолинейное, то пройденный телом путь совпадает по величине с перемещением тела.

------------------

2). Связь угловой и линейной скорости тела:

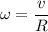
$\displaystyle \omega=\frac{v}{R}$

Так как R₁ = 2R, то:

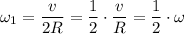
$\displaystyle \omega_{1}=\frac{v}{2R}=\frac{1}{2} \cdot\frac{v}{R}=\frac{1}{2}\cdot\omega$

То есть, при увеличении радиуса окружности в 2 раза и сохранении линейной скорости тела его угловая скорость уменьшится в 2 раза.

4,5(47 оценок)

Ответ:

baka8

22.07.2020

Объяснение: Дано: N0=1010, t=3200 лет, T=1600 лет, N−? Решение задачи: Согласно закону радиоактивного распада, число нераспавшихся ядер N, содержащихся в образце в произвольный момент времени t, можно определить через начальное число ядер в образце N0 и период полураспада T, по следующей зависимости:

Источник: http://easyfizika.ru/zadachi/kvanty-atom-atomnoe-yadro/imeetsya-10-10-atomov-radiya-skolko-atomov-ostanetsya-spustya-3200-let-esli-period/

N=N0⋅2–tT Подставим данные задачи в полученную формулу и произведем расчет численного ответа (время t и период полураспада T переводить в СИ необязательно): N=1010⋅2–32001600=2,5⋅109 ответ: 2,5·109. Если Вы не поняли решение и у Вас есть какой-то во или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Источник поставьте оценку качества решения этой задачи

Источник: http://easyfizika.ru/zadachi/kvanty-atom-atomnoe-yadro/imeetsya-10-10-atomov-radiya-skolko-atomov-ostanetsya-spustya-3200-let-esli-period/

4,7(22 оценок)

Это интересно:

Дом-и-сад

08.01.2020

Как подготовить квартиру к отъезду: советы от профессионалов...

Здоровье

03.04.2021

Как вылечить прищемленный палец: лечение дома и медицинские советы...

Семейная-жизнь

28.05.2021