1. а)420 м можно поднять 1 кг воды. я взяла формулу Энергию потенциально поднятого тела (E=mgh) вместо (Е) подставила Q (это фактически одно и тоже) и взяла массу 1 кг и ускорение 10 H/кг или м/с²
б). 210 м
2. они встретятся где-то между 30 минутами (после отправления первого поизда) и 35 минутами (после отправления первого поизда) (графики на фото)
3.
а
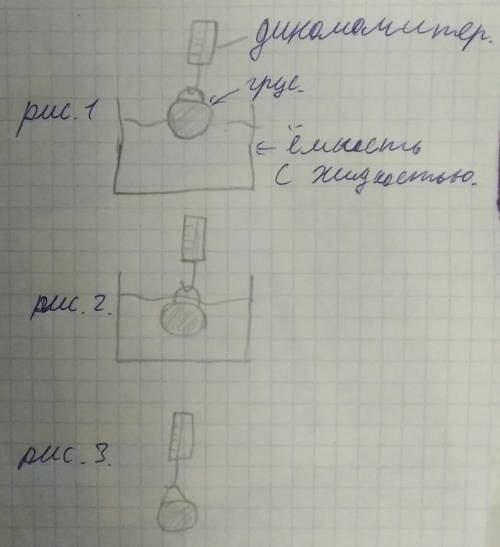
1) Измеряем вес (НЕ МАССУ) тела (смотри рис.3).
2) медленно пагружаем тело в жидкость (смотри рис.1).
3) смотрим как изменяются показания динамометра, чем они становятся меньше от веса тела тем гуще жидкость.
б
1) погружаем тело полностью в жидкость (смотри рис. 2)
2) и начинаем постепенно с равномерной скоростью поднимать при динамометра.
3) Смотрим на показания динамометра, чем они становятся больше от веса тела тем гуще жидкость
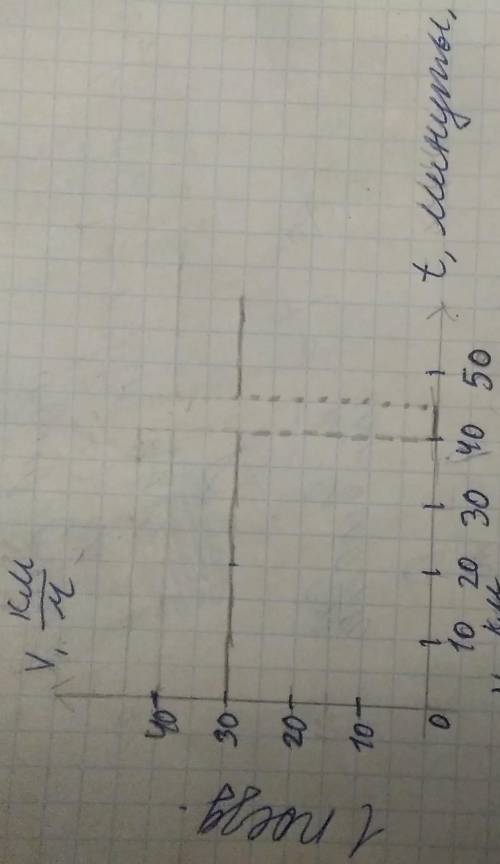

1. а)420 м можно поднять 1 кг воды. я взяла формулу Энергию потенциально поднятого тела (E=mgh) вместо (Е) подставила Q (это фактически одно и тоже) и взяла массу 1 кг и ускорение 10 H/кг или м/с²
б). 210 м
2. они встретятся где-то между 30 минутами (после отправления первого поизда) и 35 минутами (после отправления первого поизда) (графики на фото)
3.
а
1) Измеряем вес (НЕ МАССУ) тела (смотри рис.3).
2) медленно пагружаем тело в жидкость (смотри рис.1).
3) смотрим как изменяются показания динамометра, чем они становятся меньше от веса тела тем гуще жидкость.
б
1) погружаем тело полностью в жидкость (смотри рис. 2)
2) и начинаем постепенно с равномерной скоростью поднимать при динамометра.
3) Смотрим на показания динамометра, чем они становятся больше от веса тела тем гуще жидкость
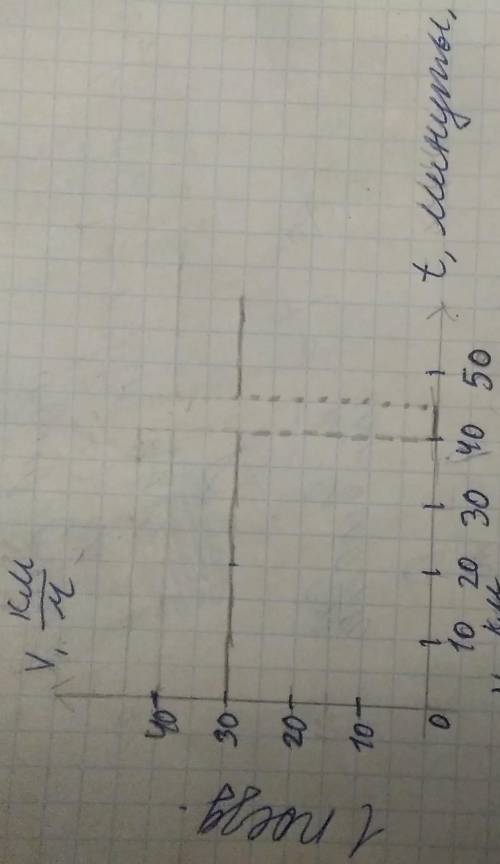


p/p0=ρ/ ρ0=e^(-z/H),
где z- высота исследуемого слоя воздуха (в метрах; вверх от поверхности Земли)
p – давление в исследуемой точке
p0 – давление у поверхности Земли
ρ и ρ0 – плотности в исследуемой точке и у поверхности
e – основание натурального логарифма, равное 2,718
H – высота однородной атмосферы, т. е. , такая высота, которую имел бы слой воздуха, если бы он был несжимаем. Она равна 8425 м.
Однако эта формула не дает взаимосвязи плотностей с температурой в явном виде. Для этого используется другая формула:
ρ/ρ0=(1-(β• z /T0))^((T0•γ0/ β• p0)-1)
здесь β – градиент температуры, град/м, т. е, величина, показывающая на сколько градусов изменяется температура при изменении высоты z на один метр;
T0 – температура у пов-сти Земли
γ0 – удельный вес воздуха, Н/м^3.
Поскольку из условия задачи температура с высотой не меняется, то ее градиент β равен 0. Из второй формулы получим
ρ/ρ0=(1-0)^∞ =1, т. е, плотность с высотой так же не меняется, а зависит только от давления. Тогда остается справедливым уравнение 1. Подставляя в нее значения, имеем
p/p0 =2,718^(-(-1000)/8425)=1,126.
Тогда давление на интересующей нас высоте
p =1,126p0.
Вот примерно так))) )