Пусть движение происходит вдоль оси z, а 0 находится на уровне земли.
Тогда уравнение движения первого тела: 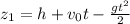 , его скорость:
, его скорость: 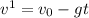
уравнение движения второго тела: 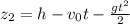
Пусть первое тело достигло максимальной высоты в момент времени 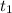 . В этот момент его скорость равна
. В этот момент его скорость равна  . Или
. Или 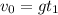
Подставим значение 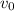 в уравнение движения первого тела в момент времени
в уравнение движения первого тела в момент времени 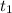 , которое в этот момент находилось на высоте Н:
, которое в этот момент находилось на высоте Н:
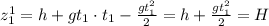
и в уравнение для второго, которое находилось на земле: 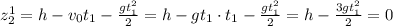 . Или
. Или 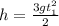
Из уравнения для первого тела: 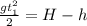 подставим в уравнение для второго:
подставим в уравнение для второго: 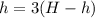 .
.
Получаем: 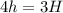 . Тогда:
. Тогда: 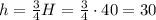 м.
м.
Найдем начальную скорость из выражения: 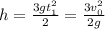 .
.
Получаем: 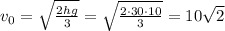 м/с.
м/с.
Потенциал большой капли равен 24,8 В
Объяснение:
ДАНО: СИ:
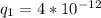 Кл
Кл
 Кл
Кл
 Кл
Кл
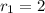 мм
мм  м
м
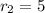 мм
мм  м
м
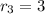 мм
мм 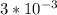 м
м
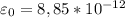 Ф/м - электрическая постоянная
Ф/м - электрическая постоянная
НАЙТИ: 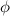 - потенциал большой капли
- потенциал большой капли
Потенциал большой капли равен  , где
, где
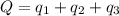 - заряд большой капли равен сумме зарядов маленьких капель,
- заряд большой капли равен сумме зарядов маленьких капель,
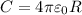 - заряд и емкость большой капли.
- заряд и емкость большой капли.
Радиус большой капли найдем из условия:
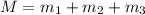 - масса большой капли ртути, равна сумме масс маленьких капель.
- масса большой капли ртути, равна сумме масс маленьких капель.
Массу можно вычислить по формуле 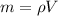 , а поскольку капли ртути имеют форму сферы, то и объем капли можно вычислить по формуле объема сферы:
, а поскольку капли ртути имеют форму сферы, то и объем капли можно вычислить по формуле объема сферы: 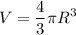 . Используем эти формулы для записи масс большой и маленьких капель ртути
. Используем эти формулы для записи масс большой и маленьких капель ртути
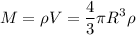
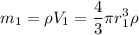
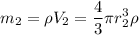
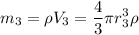 .
.
Тогда 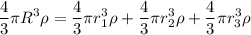
Поделим все выражение на 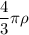 :
:
 или
или ![\displaystyle R=\sqrt[3]{r_1^3+r_2^3+r_3^3}](/tpl/images/2115/0739/6e85b.png) .
.
Подставим полученные выражения для Q, C и R в уравнение потенциала 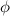 получаем:
получаем:
![\displaystyle \phi=\frac{q_1+q_2+q_3}{4\pi \varepsilon_0\sqrt[3]{r_1^3+r_2^3+r_3^3} }](/tpl/images/2115/0739/db6e5.png)
Это итоговая формула.
Вычислим значение потенциала большой капли ртути
![\displaystyle \phi=\frac{4*10^{-12}+5*10^{-12} +6*10^{-12} }{4*3,14*8,85*10^{-12} *\sqrt[3]{(2*10^{-3})^{3} +(5*10^{-3})^{3} +(3*10^{-3})^{3} } }](/tpl/images/2115/0739/51841.png)
![\displaystyle \phi=\frac{(4+5+6)*10^{-12} }{4*3,14*8,85*10^{-12} *\sqrt[3]{(8+125+27)*10^{-9} } } =\frac{15*10^3}{603,58}=24,8](/tpl/images/2115/0739/22053.png) (В)
(В)
2.V=V0+at
3.x=x0+Vt
x=x0+Vt
4.x=x0+V0t+(at²)/2
x=x0+V0t-(at²)/2
5.