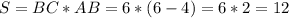см²
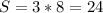
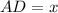. Тогда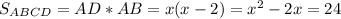 
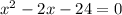. По теореме Виета находим его корни: 
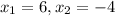. Так как длина не может быть отрицательной, то выбираем первый корень. 
. 
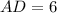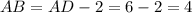см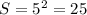
.
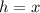. Тогда наша сторона будет равна 
. Учитывая, что площадь треугольника равна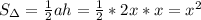 
, приравняем это к площади квадрата.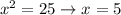
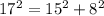, что делает наш треугольник прямоугольным. Две высоты будут равны соответственно катетам, а третью мы найдем через площадь. Вот как: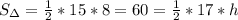
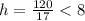. ответ: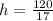 
Объяснение:
Могут, если прямая с не лежит в плоскости, содержащей пересекающиеся прямые а и b .
Через параллельные прямые можно провести плоскость, притом только одну. Плоскость, содержащая а и с, пересечет плоскость, содержащую пересекающиеся а и b.
Тогда прямые с и b не параллельны и не имеют общих точек – они скрещивающиеся.