если острый угол ромба равен 60° то тупой 120°, проведем диагональ ВD, она разделит ромб на два правильных треугольника, т.к. она является биссектрисой его внутренних углов и потому все углы в этих треугольниках по 60°, а коль так, то сторона ромба равна диагонали, а периметр = 4*15=60/см/
 .
.
1), 2), 6), 8).
Объяснение:
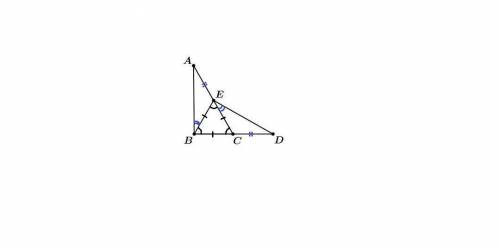
ΔАВС = ΔDEB,
АВ = DE, АС = DB, значит ВС = ВЕ, т.е. ΔВЕС равнобедренный
В равных треугольниках против равных сторон лежат равные углы, значит
∠DBE = ∠ACB, тогда
ΔВЕС равнобедренный с основанием ВС.
Итак, ВЕ = ЕС = ВС, т.е. ΔВЕС равносторонний.
∠АВЕ = ∠АВС - ∠ЕВС
∠DEC = ∠DEB - ∠BEC
∠АВС = ∠DEB из равенства треугольников,
∠EBC = ∠BEC, как углы равностороннего треугольника, значит
∠АВЕ = ∠DEC.
АЕ = АС - ЕС
CD = DB - BC
AC = DB по условию,
ЕС = ВС, так как ΔВЕС равносторонний, значит
АЕ = CD.
1) Треугольник BCE равнобедренный - верно.
2) Треугольник BCE равносторонний - верно.
3) ∠ABC = 90° - нельзя утверждать.
4) Треугольник ECD равнобедренный - нельзя утверждать.
5) AE = BC - нельзя утверждать.
6) AE = CD - верно.
7) ∠ABE = ∠CDE - нельзя утверждать.
8) ∠ABE = ∠CED - верно.
Так как в ромбе все стороны равны, то ΔАВД - равнобедренный.
Так как в равнобедренном треугольнике один из углов равен 60°, то этот треугольник равносторонний . Значит, АВ=АД=ВД=15 см. И все стороны ромба тоже равны 15 см.
Периметр ромба равен 15*4=60 см .