∠XIaY=114°
Объяснение:
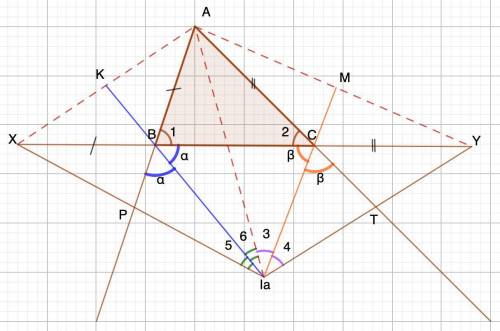
Дано: ΔАВС.
BIa - биссектриса ∠РВС; СIa - биссектриса ∠ВСТ;
ХВ=АВ; АС=СY;
∠ВАС=66°.
Найти: ∠XIaY
1. ∠1+∠2=180°-66°=114° (сумма углов Δ)
∠1+2α=180° (развернутый)
∠2+2β=180° (развернутый)
∠1+∠2+2α+2β=360°
2(α+β)=360°-114°=246° ⇒ α+β=123°
2. Рассмотрим ΔBCIa.
∠BIaC=180°-(α+β)=180°-123°=57° =∠6+∠3 (сумма углов Δ)
3. Рассмотрим ΔХВА - равнобедренный.
∠XBA=∠KBA=α ⇒ ВК - биссектриса, медиана, высота (свойство р/б Δ)
4. Рассмотрим ΔACY - равнобедренный.
∠АСМ=∠MCY=β ⇒ CM - биссектриса, медиана, высота (свойство р/б Δ)
5. Рассмотрим ΔXIaA.
IaK - высота, медиана (п.3) ⇒ ΔXIaA - равнобедренный
⇒ IaK - биссектриса ⇒ ∠5=∠6.
6. Рассмотрим ΔAIaY.
IaM - высота, медиана ⇒ ΔAIaY - равнобедренный
⇒ IaM - биссектриса ⇒ ∠3=∠4
7. ∠XIaY=∠5+∠6+∠3+∠4=2*(∠6+∠3)=2*57°=114°
ответ:Если два отрезка пересекаются,то это выглядит так
Х
При пересечении отрезков получаются четыре вертикальных угла,противоположные углы равны между собой
А тут ещё речь идёт о треугольниках,и из условия известно,что отрезки пересекаются в точке О,которая является серединой каждого из них
Из условия задачи следует,что
ВО=ОК
АО=ОМ
И углы между сторонами равны,как вертикальные
Треугольники равны по первому признаку равенства треугольников-если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника,то эти треугольники равны между собой
Объяснение:
ответ:28
Объяснение:
P=2*(a+b)
P=2*(10+4)=2*(14)=28