Объяснение:
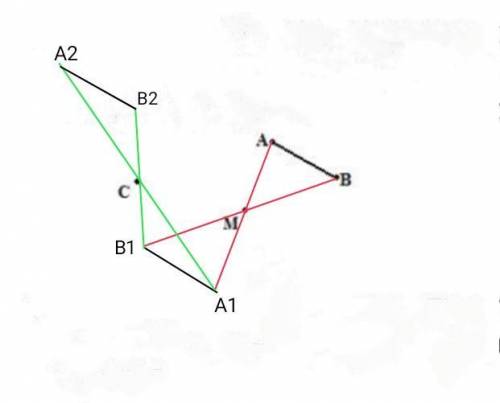
Берём линейку и отмеряем расстояние АМ от точки М отмеряем расстояние такое же как расстояние АМ и откладываем точку А1. (Можно использовать циркуль провести от точки А прямую проходящую через т.М. циркулем отмерить расстояние АМ и провести полуокружность точка пересечения с прямой и будет точкой А1)
Так делаем с каждой точкой.
На рисунке погрешность, вы должны сделать равные отрезки
АМ=МА1
МВ=МВ1
А1С=СА2
В1С=СВ2
(для этого используется линейка или циркуль)
У вас не должно быть погрешности, поскольку, вы, будете использовать линейку.
1) пусть x - это катет в левой части трапеции с острым углом 30°
пусть y - это катет в правой части трапеции с острым углом 60°
на них приходится 15 - 7 = 8см, следовательно, x + y = 8
выясним, как связаны x и y
tg60 = h / y => y = h / tg60 = h / √3
tg30 = h / x => x = h / tg30 = 3h / √3
заметим, что x > y в 3 раза
пусть x = 3a, y = a
тогда 3a + a = 8,
a = 2
следовательно, x = 6, y = 2
теперь через тот же тангенс найдем высоту трапеции:
tg60 = h / y => h = tg60 y = 2√3.
2) по теореме Пифагора найдем диагонали трапеции
d1 = sqrt(9² + (2√3)²) = √93
d2 = sqrt(13² + (2√3)²) = √181