ответ:Самая последняя это формула Герона где р-это полупериметр
р=а+в+с/2 где а,в,с стороны треугольника
S=1/2ah это произведение половины стороны треугольника (а) на высоту ( h)проведенную к этой стороне
S=1/2 ab siny Это площадь ∆ равна половине произведения двух его сторон на синус угла между ними
Объяснение:
S=a^2*√3/4
Это формула площади равностороннего треугольника где а-сторона
обозначим вершины ромба буквами a, b, c, d. буквой o обозначим точку пересечения диагоналей.
угол dab = 120о. отсюда следует, угол oab = 60о, так как диагональ ас делит угол пополам.
так как у нас ромб разбит на прямоугольные треугольники, рассмотрим треугольник oab.
мы знаем, что угол oab = 60о. значит угол аво = 30о.
так как в точке пересечения диагонали ромба делятся пополам, имеем ао = 0,5 ас. получаем ао = 0,5 * 4,5 = 2,25 см.
напротив угла 30о лежит катет. что равен половине гипотенузы.
если ао = 2,25 см, то ав, являясь гипотенузой прямоугольного треугольника, будет равна 2 * ао
ав = 2 * 2,25 = 4,5 см.
нам известно, что у ромба все стороны равны.
периметр ромба составит р = 4 *ав, з = 4 * 4,5 см = 18 см.
ответ: периметр ромба составляет 18 см
проекции перпендикулярны, тогда по т Пифагора расстояние между точками пересечения наклонными плоскости равно sqrt{18}, так как угол между наклонными равен 60, наклонные равны (так как проекции равны), то наклонные и линия, соединяющая точки пересечения с плоскостью образуют правильный тр-к => гипотенуза прямоуг тр-ка, образованного одной наклонной, перпендикуляром, опущенным из данной точки на плоскость и проекцией этой наклонной, равна sqrt{18}. По т Пифагора, перпендикуляр равен sqrt{18-9} = 3

В решении задачи можно использовать любую из формул, в зависимости от условия задачи .
Формула площади равностороннего треугольника со стороной а - это
Если известны две стороны треугольника и угол между ними, то можно воспользоваться формулой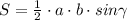 .
.
Формула площади , если известны сторона треугольника и высота, опущенная на эту сторону: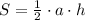 .
.
Формула Герона: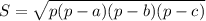 .
.