Ромб - стороны равны, противоположные углы равны, диагонали перпендикулярны.
Треугольники ABE и CBF равны по гипотенузе и острому углу, AE=CF.
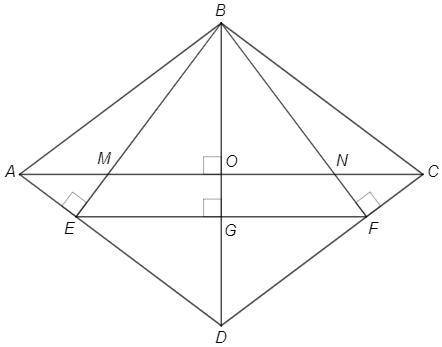
Точки E и F делят стороны ромба в равном отношении => AC||EF => EF⊥BD
S(ABO) =1/4 S(ABCD) =1/4 *1/2 *160*120 =2400
AB =√(AO^2 +BO^2) =100
∠ABD=∠ADB => △ABO~△BDE
BE/AO =BD/AB => BE =80*120/100 =96
△BEG~△BMO~△BDE => △BEG~△BMO~△ABO
S(BEG)/S(ABO) =(BE/AB)^2 =(96/100)^2 =0,96^2
S(BMO)/S(ABO) =(BO/AO)^2 =(60/80)^2 =0,75^2
S(MOGE) =S(BEG)-S(BMO) =2400 (0,96^2 -0,75^2) =861,84
S(MNFE) =2 S(MOGE) =1723,68
ответ: переведено с программы-переводчика, русская оригинальная версия в объяснении
(Точка М на малюнку відповідає точці E в даній задачі)
Так як бісектриса кута паралелограма відсікає від нього рівнобедрений трикутник, то АВ = ВЕ = 7 см
У параллелограмме всі сторони попарно рівні і паралельні.
З цього випливає, що AD = ВС = 12 см
ЕС = ВС - ВЕ = 12 - 7 = 5 см
Відповідь: BE = 7 см і EC = 5 см
Объяснение:
(Точка М на рисунке соответствует точке E в данной задаче)
Так как биссектриса угла параллелограмма отсекает от него равнобедренный треугольник, то АВ = ВЕ = 7 см
В параллелограмме все стороны попарно равны и параллельны.
Из этого следует, что AD = ВС = 12 см
ЕС = ВС - ВЕ = 12 - 7 = 5 см
ответ: BE = 7 см и EC = 5 см

Sпрямоугольника=32 кв единицы
S полукруга=πR²/2=3,14*4/2=6,28
Sчетверти круга=πR²/4=3,14*16/4=12,56
Sзаштр.=32-6,28-12,56=13,16 кв. единиц.