не будет дискриминанта
Объяснение:
D=b^2-4ac=16-80
ответ: r=12 см
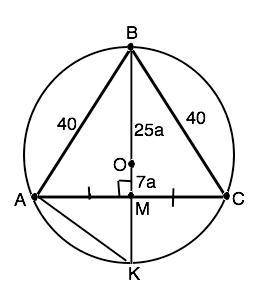
Объяснение: Обозначим данный треугольник АВС, ВМ - медиана, О - центр описанной окружности, ВК - диаметр.
Медиана равнобедренного треугольника к основанию является его высотой и биссектрисой.⇒ ВМ⊥АС.
Примем коэффициент отношения отрезков медианы равным а. Тогда ВО=25а, ОМ=7а.
∠КАВ – вписанный, ВК - диаметр, ⇒ ∆ ВАК прямоугольный, АМ - его высота. Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.⇒ АМ²=КМ•ВМ.
ОК=ОВ=25а - радиусы. ⇒ ВМ=ВО+ОМ=25а+7а=32а; МК= ОК-ОМ=25а-7а=18а. ⇒ АМ²=32а•18а=576а², откуда AM=√576a²=24a.
Из прямоугольного ∆ АВМ по т.Пифагора АМ²+ВМ²=АВ², т.е. 24а²+32а*=1600, откуда а=1 см.
Формула радиуса вписанной в треугольник окружности r=S/p, где Ѕ - площадь треугольника. р - его полупериметр. r=0,5•ВМ•АС:0,5(АВ+ВС+АС)=12 см
ответ: 26
Объяснение:
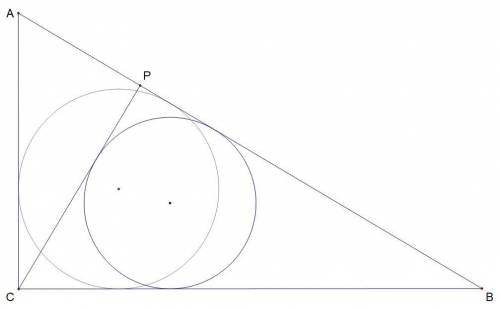
Пусть r -- радиус вписанной окружности в ΔBCP, а R -- радиус вписанной окружности в ΔBAC
1.
tg∠BAC = 12/5, откуда по определению тангенса
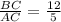
Пусть BC = 12x, тогда AC = 5x
По теореме Пифагора найдём AB:
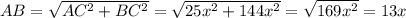
2.
tg∠CAP = 12/5, по определению тангенса из ΔACP
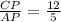
Пусть CP = 12y, тогда AP = 5y
Составим уравнение с теоремы Пифагора в ΔACP и выразим y через x:

Отрицательным y быть не может, так как он выражает длину отрезка, следовательно y = 5x/13, откуда
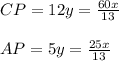
3. Выразим через x сторону BP, периметр и площадь ΔCPB:
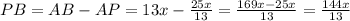
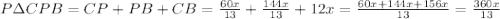
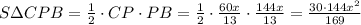
4. Используя формулу площади через радиус вписанной окружности составим уравнение:

5. Используя найденный x, вычислим периметр и площадь ΔABC:
PΔabc = AB + BC + AC = 13x + 12x + 5x = 30x = 30*13
SΔabc = 1/2 * AC * CB = 1/2 * 5x * 12x = 30x² = 30*13²
6. Найдём R, составив уравнение по формуле S = P/2 * R
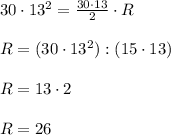
ответ: дискриминант 4²-4*2*10=16-80=-64. Всё просто.
Объяснение: