Докажи, что четырёхугольник abcd является прямоугольником, найди его площадь, если a(12; 2) , b(18; 8) , c(12; 14) и d(6; 8) .
sabcd=
2.
условие : 4 б.
дан треугольник abc и координаты вершин этого треугольника. определи длины сторон треугольника и укажи вид этого треугольника.
a(-8; 1), b(-5; 5) и c(-2; 1).
ab =
;
bc =
;
ac =
.
треугольник abc
равносторонний
равнобедренный
разносторонний
3точка a находится на положительной полуоси ox , точка b находится на положительной полуоси oy .
нарисуй прямоугольник aobc и диагонали прямоугольника. определи координаты вершин прямоугольника и точки d пересечения диагоналей, если длина стороны oa равна 14,1, а длина стороны ob равна 2,3.
a()
o()
b()
c()
d()
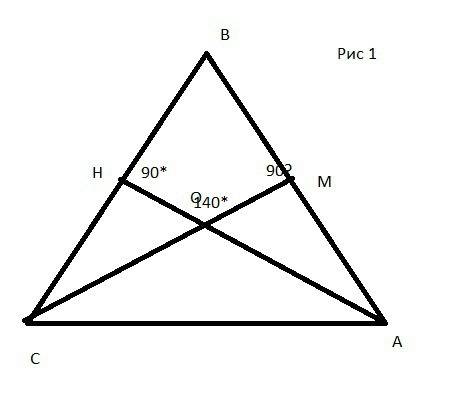
В тр-ке ЕАВ опустим высоту ЕМ, а в тр-ке ЕМС проведём высоту МК. М∈АВ, К∈ЕС.
В тр-ке ЕАВ ЕМ=ab/c=ЕА·ЕВ/АВ=(7√2)²/14=7 см.
В правильном тр-ке АВС высота СМ=а√3/2=14√3/2=7√3 см.
Высота пирамиды ЕО опускается в центр вписанной в основание окружности. r=МО=СМ/3=7√3/3 см.
В тр-ке ЕМО ЕО=√(ЕМ²-МО²)=√(7²-(7√3/3)²)=7√6/3 см.
Площадь тр-ка ЕМС можно вычислить двумя через высоты ЕО и МК, запишем их, сразу приравняв друг к другу:
СМ·ЕО/2=ЕС·МК/2,
МК=СМ·ЕО/ЕС,
МК=(7√3·7√6)/(3·7√2)=7√18/3√2=7√9/3=7 см.
МК - расстояние между скрещивающимися рёбрами АВ и ЕС. В правильной пирамиде все подобные расстояния равны.
ответ: 7 см.