Углы, образованные при пересечении двух параллельных прямых секущей, или равны, или в сумме составляют 180°. Следовательно, нам дано значение одного из смежных углов.
а) второй угол равен 180° - 150° =30°.
б) один из углов равен Х градусов, второй - Х+70 градусов. Их сумма равна 2Х+70=180° => X=55°. Тогда меньший угол = 55°, второй = 125°.
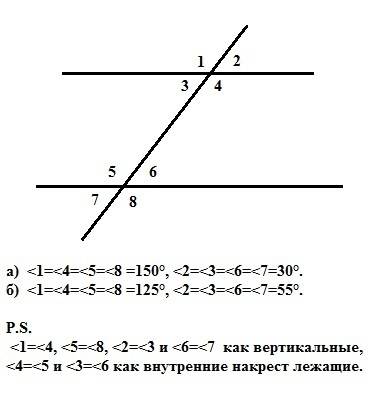
Или (см. рисунок): а) <1=<4=<5=<8 =150°, <2=<3=<6=<7=30°.
б) <1=<4=<5=<8 =125°, <2=<3=<6=<7=55°.
P.S.
<1=<4, <5=<8, <2=<3 и <6=<7 как вертикальные,
<4=<5 и <3=<6 как внутренние накрест лежащие.
Пусть СВ=3Х, АВ=5Х. По Пифагору (5Х)²-(3Х)² = АС². Отсюда Х=1.
Высота, проведенная из вершины прямого угла на гипотенузу, делит данный тр-к на два подобных друг другу и исходному. Из подобия имеем соотношение:
АВ/СВ=СВ\НВ. Откуда НВ= СВ²/АВ = 9/5 = 1,8.
2) Синус угла это отношение противолежащего катета к гипотенузе, то есть СВ/АВ=3/5. Их подобия тр-ков имеем: АВ/СВ=СВ/НВ или АВ= СВ²/НВ.
СВ=3Х, АВ=5Х подставляем: 5Х=9Х²/1,8, откуда Х=1. Значит АВ = 5.