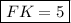
Объяснение:
Дано: 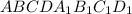 - правильная усеченная четырехугольная пирамида,
- правильная усеченная четырехугольная пирамида, 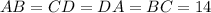 ,
, 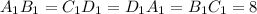 ,
, 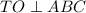 ,
, 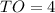 , AK = KB,
, AK = KB, 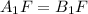
Найти: FK - ?
Решение: По свойствам правильной усеченной четырехугольной пирамиды 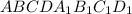 её основаниями являются квадраты, а высота пирамиды проходит через центры квадратов. Так точка O - точка пересечения диагоналей квадрата ABCD, то диагонали точкой пересечения делятся пополам по свойствам квадрата. Так как диагонали квадрата равны по теореме, то и половины диагоналей также равны, тогда AO = OB и треугольник ΔAOB - равнобедренный. Так как для треугольника ΔAOB отрезок OK - медиана
её основаниями являются квадраты, а высота пирамиды проходит через центры квадратов. Так точка O - точка пересечения диагоналей квадрата ABCD, то диагонали точкой пересечения делятся пополам по свойствам квадрата. Так как диагонали квадрата равны по теореме, то и половины диагоналей также равны, тогда AO = OB и треугольник ΔAOB - равнобедренный. Так как для треугольника ΔAOB отрезок OK - медиана
(по условию AK = KB), то по теореме медиана равнобедренного треугольника проведенная к основания является биссектрисой и высотой. Треугольник ΔBOK подобен треугольнику ΔBDA по двум углам так как угол ∠OBK - общий и OK ⊥ AB, и DA ⊥ AB.
Так как ΔBOK подобен треугольнику ΔBDA:
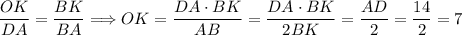 .
.
Так как квадрат ABCD подобен квадрату  так как все углы квадрата равны 90°, то можно записать отношения соответствующих элементов квадрата:
так как все углы квадрата равны 90°, то можно записать отношения соответствующих элементов квадрата:
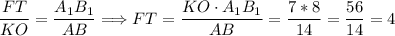 .
.
TFOK - трапеция так как FT║OK по свойствам правильной усеченной четырехугольной пирамиды 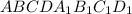 . Рассмотрим трапеция TFOK.Трапеция TFOK - прямоугольная так как по условию
. Рассмотрим трапеция TFOK.Трапеция TFOK - прямоугольная так как по условию 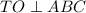 и OK ⊂ ABC .Проведем высоту из точки F в точку H на основании OK. Так как FH - высота трапеции и TO - высота трапеции, то FH = TO = 4. По свойствам трапеции четырехугольник TOHF - прямоугольник, тогда его противоположные стороны равны по свойствам прямоугольника и TF = OH = 4. OK = OH + HK ⇒ HK = OK - OH = 7 - 4 = 3. Рассмотрим прямоугольный (FH ⊥ OK по построению) треугольник ΔFHK. По теореме Пифагора:
и OK ⊂ ABC .Проведем высоту из точки F в точку H на основании OK. Так как FH - высота трапеции и TO - высота трапеции, то FH = TO = 4. По свойствам трапеции четырехугольник TOHF - прямоугольник, тогда его противоположные стороны равны по свойствам прямоугольника и TF = OH = 4. OK = OH + HK ⇒ HK = OK - OH = 7 - 4 = 3. Рассмотрим прямоугольный (FH ⊥ OK по построению) треугольник ΔFHK. По теореме Пифагора: 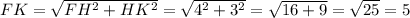 .
.

ОбъясОкружность
Cамая простая из всех кривых линий - окружность. Это одна из древнейших геометрических фигур. Философы древности придавали ей большое значение. Согласно Аристотелю, небесная материя, из которой состоят планеты и звезды, как самая совершенная, должна двигаться по самой совершенной линии - окружности. Сотни лет астрономы считали, что планеты двигаются по окружностям. Это ошибочное мнение было опровергнуто лишь в XVII веке учением Коперника, Галилея, Кеплера и Ньютона.
В Древней Греции круг и окружность считали венцом совершенства. В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности стало толчком к возникновению колеса, так как ось и втулка колеса должны всё время быть в соприкосновении.
Если остановится колесо, то остановится колесо Истории. Остановятся все виды транспорта, остановятся все часы и механизмы, фабрики и заводы. Не произойдет движения вперед.
Итак, что же такое окружность? Какими свойствами она обладает???
Вот это и предстоит нам узнать...
Из истории окружности
Самая простая из всех кривых линий - окружность. Это одна из древнейших геометрических фигур. Философы древности придавали ей большое значение. Согласно Аристотелю, небесная материя, из которой состоят планеты и звезды, как самая совершенная, должна двигаться по самой совершенной линии - окружности.
Для первобытных людей важную роль играла форма окружающих их предметов. По форме и цвету они отличали съедобные грибы от несъедобных, пригодные для построек деревья и деревья, которые годятся лишь на дрова, вкусные орехи от горьких или ядовитых. Особенно вкусны орехи кокосовой пальмы. Эти орехи очень похожи на шар. А добывая каменную соль или горный кварц, люди наталкивались на кристаллы, потом научились шлифовать их. Отшлифованные орудия позволили быстро срубить дерево, разрезать мясо лучше охотиться на зверей. Специальных названий для геометрических фигур тогда не было. Говорили: “Такой, как кокосовый орех”, (т. е. круглый), “такой, как соль” (т. е. имеющий форму куба). Некоторые формы фигур казались особо красивыми. И действительно, нельзя без восхищения смотреть на красоту кристаллов, цветов, фигур, имеющих правильную круглую форму. Только в Древней Греции окружность и круг получили свои названия.
Круглые тела в древности заинтересовали человека. Так в Древнем Египте для постройки знаменитых египетских пирамид никаких технических сооружений еще не было. Даже шлифовать огромные каменные глыбы приходилось вручную, а перемещали их с бревен круглой формы. Позже вместо бревен стали использовать их части – в виде колес, которые катились уже легче.нение:
Круг
Однажды, в далеком 1972 году два англичанина, Артур Шаттлвуд и Брюс Бонд, прекрасной лунной ночью сидели на склоне холма, пытаясь увидеть хоть одну малюсенькую летающую тарелочку, но стали очевидцами несколько более экстраординарного события - в сотне метров от себя они увидели, как неожиданно часть колосьев веерообразно полегла, образовывая идеальный круг. С того момента сообщения о появлении таинственных кругов на полях стали поступать с завидной регулярностью. Сейчас насчитывается уже более 9 000 сообщений о феномене, 90% из которых приходится на Англию. Статистику не стоит считать верной, не все представляют, с чем они столкнулись, а даже если и представляют, то не знают, куда обращаться. Круги появлялись повсеместно, но территория Англии словно была любимым местом "для пикников" НЛО, притягивая внимание ученых, исследователей и, конечно же, фальсификаторов