Прямые BD и m - скрещивающиеся прямые.
Объяснение:
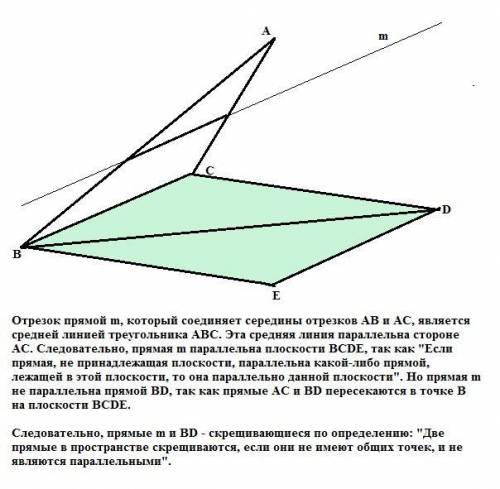
Отрезок прямой m, который соединяет середины отрезков AB и AC, является средней линией треугольника АВС. Эта средняя линия параллельна стороне АС. Следовательно, прямая m параллельна плоскости ВСDE, так как "Если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельно данной плоскости". Но прямая m не параллельна прямой BD, так как прямые АС и BD пересекаются в точке В на плоскости BCDE.
Следовательно, прямые m и BD - скрещивающиеся по определению: "Две прямые в пространстве скрещиваются, если они не имеют общих точек, и не являются параллельными".
Диагонали в равнобедр. трапеции образуют собой равнобедр. треугольники AOD и BOC рассмотри треугольник ВОС:
угол ВОС равен 180- 60= 120, тогда углы при основании равны по 30 (углы ОСВ и ОВС)
далее возьмем прямоугольный треугольник АНС где АН- высота:
угол АСН мы нашли он равен совпадающему углу ОСВ и равен 30
тогда угол НАС равен
180-90-30=60
АН=2
найдем сторону НС:
по формуле НС = АН*tgА= 2* tg HAC= 2 * tg 60 = 2* корень из 3=
2 корня из 3
окей, далее найдем АС она же является диагональю трапеции:
АС= НС/sin НАС= 2 корня из 3/ ( 1/2* корень из 3) = 4
готово, осталось посчитать:
S = АС^2 /2 * sin 60= 8* корень из 3 /2 = 4 корня из 3 см в квадрате