ответ: S=20см²
Объяснение: Обозначим вершины трапеции А В С Д а точки касания К М Е Т, центр окружности О. стороны трапеции являются касательными к вписанной окружности и отрезки касательных соединяясь в одной вершине, равны от вершины до точки касания, поэтому ВК=ВМ=МС=СЕ=1см;
АК=АТ=ЕД=ТД=4см. Сложим эти цифры и получим стороны трапеции:
АВ=СД=4+1=4см; ВС=1+1=2см;
АД=4+4=8см.
Проведём из вершин верхнего основания к АД две высоты ВР и СН. Они делят АД так что РН=ВС=2см. Так как трапеция равнобедренная то:
АР=ДН=(АД-ВС)/2=(8- 2)÷2=6÷2=3см
АР=ДН=3см. Рассмотрим полученный ∆СДН. В нём СД -гипотенуза, а СН и ДН- катеты. Найдём высоту СН по теореме Пифагора: СН²=СД²-ДН²=
=5²-3²=25-9=16; СН=√16=4см
СН=4см. Теперь найдём площадь трапеции зная высоту и оба основания по формуле:
S=(BC+AД)/2×СН=
=(2+8)/2×4=10÷2×4=5×4=20см²
S=20см²
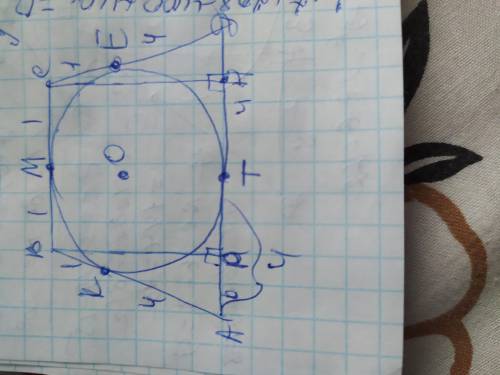
пусть ad> bc , тогда острые углы равные 75 и 15 гр лежат при оснований ad , положим что y,w середины сторон ab и cd соответственно , тогда yw средняя линия трапеции , значит ad+bc=2yw из условия мы знаем что yw равна либо 15 либо 7 , положим что ab и cd пересекаются в точке e , тогда aed=180-(75+15)=90 , положим также что z,x это середины сторон основании bc,ad соотвественно , пусть n точка пересечения yw и zx , тогда по замечательному свойству трапеции точки e,z,x лежат на одной прямой , учитывая что угол aed прямой , получаем что ax=ex=ad/2 , ez=bz=bc/2 , но так как ex=ez+zx откуда окончательно получаем две системы
{ad-bc=2*7
{ad+bc=2*15
или
{ad-bc=2*15
{ad+bc=2*7
подходит решение первой системы , так как они положительны , складывая получаем ad=22 , bc=8 , значит ответ bc=8.