1) Дано: МE=ED , EF=EC , MD пересекается с CF в точке Е .
Доказать: ΔMEF=ΔDEC .
Решение. Так как МE=ED , EF=EC , ∠MEF=∠CED (как вертикальные) , то треугольники равны по 1 признаку
2) Дано: BC=DC , AB=AD . Док-ть: ΔADC=ΔABC .
BC=DC , AB=AD , AC - общая сторона ⇒ равенство треугольников по 3 признаку
3) Дано: ∠ВАС=∠DAC , ∠ACD=∠ACB . Док-ть: ΔABC=ΔADC . ∠ВАС=∠DAC , ∠ACD=∠ACB , AC - общая сторона ⇒ равенство треугольников по 2 признаку
4) Дано: AB=BC , ∠ABD=∠CBD=90° . Док-ть: ΔABD=ΔCBD.
AB=BC , ∠ABD=∠CBD=90° , BD - общая сторона ⇒
равенство треугольников по 1 признаку .
геометрия (9 класс)
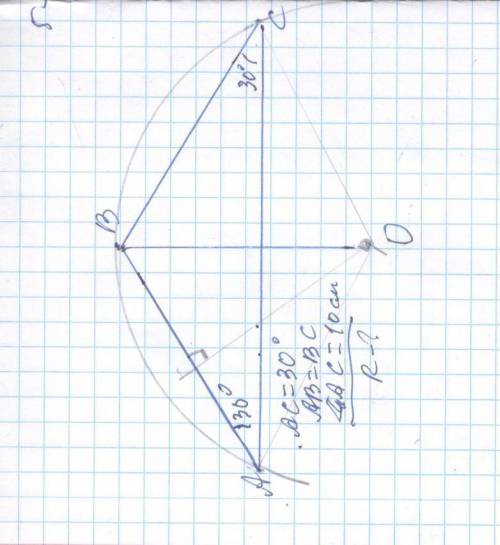
Найти длину окружности ,описанной около равнобедренного треугольника с основанием 10 см и углом 30° при основании .
Дано: ∠A = ∠C =30 ° , AC=b =10 см
----------------------------
R - ?
решение : Можно разными но геометрия (9 класс)
→ рационально использовать теорема синусов :
a/sin∠A = b /sin∠B = c /sin∠C = 2R
Угол против основания ∠B =180° - (30°+30°) = 180° - 60° 120°
AC/sin∠B =2R ⇔ R = AC/2sin∠B
R = 10 /2sin(180° - 60°) =10/2sin60° =10/ (2*√3 / 2) =10 /√3 =( 10√3) /3
Площадь боковой поверхности пирамиды равна S=1/2*P*a. Где Р-периметр основания, а-апофема. бозначим пирамиду. АВСДS, S-вершина, АД-большее основание трапеции, ВС -меньшее. Высота пирамиды SК. Проведём перпендикуляры к сторонам трапеции из точки К. К АВ перпендикуляр КЕ, к ВС КМ, к СД КF, к АД KN. Соединим вершину пирамиды М с точками Е,M,F,N. Полученные прямоугольные треугольники SКЕ, SKM,SKF,SKN равны. Поскольку их острые углы при основании равны по условию , и они имеют общий катет SK. Отсюда высоты боковых граней будут равны, то есть апофема а=5. Соединим вершины трапеции с точкой К. Треугольники КВЕ и КВМ равны по катету(ЕК=КМ) и гипотенузе(ВК). Отсюда ЕВ=ВМ. Аналогично из равенства треугольников АКЕ и АКN получаем АЕ=AN. Отсюда (AN+BM)=АД=2. То же самое в треугольниках МКС, КСF, КДF, KДN. То есть( МС+NД)=СД=4. Тогда периметр основания пирамиды равен Р=2АВ+2СД=4+8=12. Отсюда площадь боковой поверхности пирамиды S=1/2*12*5=30.