Две хорды окружности АС и BD взаимно перпендикулярны.
а) Найдите отрезок. соединяющий середины хорд АС и BD, если отрезок. соединяющий точку их пересечения с центром окружности равен 3.
б) При условии пункта а) найдите AD, если AD>BC, AC=BD и отрезок, соединяющий середины хорд АВ и CD, равен 5.
————————
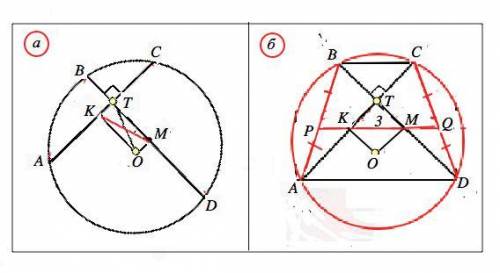
а) Обозначим середины хорд АС и ВD точками К и М соответственно. . Угол Т в точке пересечения хорд - прямой (дано).
Радиус, проведенный к середине хорды, перпендикулярен ей ⇒ Углы ОКТ-ТМТ - прямые. ⇒ Четырехугольник ОКТМ - прямоугольник. Расстояние ОТ является его диагональю. Диагонали прямоугольника равны. ⇒ Длина отрезка между центрами хорд равна КМ=ОТ=3.
---------------
б) Хорды АС и ВD равны и взаимно перпендикулярны (дано), они , стягивают равные дуги и при пересечении образуют равнобедренные прямоугольные треугольники. Поэтому хорды АВ и СD, которые соединяют концы АС и ВD, равны.
Четырехугольник АВСD - равнобедренная трапеция, и PQ - её средняя линия.
Из решения пункта а) данной задачи отрезок КМ=3. Он проходит через середины АС и ВD и принадлежит средней линии PQ. Для треугольников АВС и DBC с общим основанием ВС отрезки РК и МQ - средние линии, поэтому равны. РК=MQ=(PQ-KМ):2=(5-3):2=1. АD - основание треугольника АВD, РМ - его средняя линия. По свойству средней линии треугольника АD=2РМ=2•(PK+KM)=2•(1+3)=8 (ед. длины)
Две хорды окружности АС и BD взаимно перпендикулярны.
а) Найдите отрезок. соединяющий середины хорд АС и BD, если отрезок. соединяющий точку их пересечения с центром окружности равен 3.
б) При условии пункта а) найдите AD, если AD>BC, AC=BD и отрезок, соединяющий середины хорд АВ и CD, равен 5.
————————
а) Обозначим середины хорд АС и ВD точками К и М соответственно. . Угол Т в точке пересечения хорд - прямой (дано).
Радиус, проведенный к середине хорды, перпендикулярен ей ⇒ Углы ОКТ-ТМТ - прямые. ⇒ Четырехугольник ОКТМ - прямоугольник. Расстояние ОТ является его диагональю. Диагонали прямоугольника равны. ⇒ Длина отрезка между центрами хорд равна КМ=ОТ=3.
---------------
б) Хорды АС и ВD равны и взаимно перпендикулярны (дано), они , стягивают равные дуги и при пересечении образуют равнобедренные прямоугольные треугольники. Поэтому хорды АВ и СD, которые соединяют концы АС и ВD, равны.
Четырехугольник АВСD - равнобедренная трапеция, и PQ - её средняя линия.
Из решения пункта а) данной задачи отрезок КМ=3. Он проходит через середины АС и ВD и принадлежит средней линии PQ. Для треугольников АВС и DBC с общим основанием ВС отрезки РК и МQ - средние линии, поэтому равны. РК=MQ=(PQ-KМ):2=(5-3):2=1. АD - основание треугольника АВD, РМ - его средняя линия. По свойству средней линии треугольника АD=2РМ=2•(PK+KM)=2•(1+3)=8 (ед. длины)

Объяснение:
а)Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю. Т.К а(2; -1;8) b (-10;х; -40) , то
а*в=2*(-10)-1*х+8*(-40) , а*в=0
-20-х-320=0,
-340-20х=0
-20х=340
х=-17
б) Два вектора a и b коллинеарны ,если их координаты пропорциональны, значит если а(2; -1;8) b (-10;х; -40) , то 2/(-10)=-1/х . х=5