Sбок = 120(2+√3) см².
Объяснение:
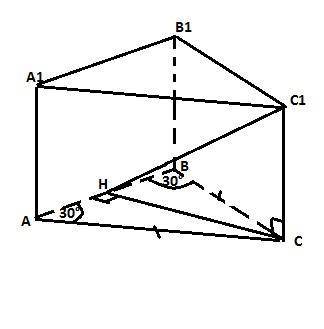
Треугольник АВС равнобедренный (АС=ВС - дано). Его высота - перпендикуляр из вершины С к стороне АВ равен половине боковой стороны, так как лежит против угла 30°.
Итак, СН = 5 см. Расстояние от вершины С1 до стороны АВ - это перпендикуляр С1Н к стороне АВ и его проекция на основание АВС - это высота СН (по теореме о трех перпендикулярах).
Тогда в прямоугольном треугольнике СНС1 катет СС1 по Пифагору равен √(С1Н²-СН²) = √(169-25) = 12 см. Это высота нашей прямой призмы. Тогда площадь ее боковой поверхности равна периметру основания, умноженному на высоту. Учитывая, что сторона АВ равна 10√3 см (из прямоугольного треугольника САН АН = 5√3 см, а
АВ = 2·АН), Sбок = (20+10√3)·12 = 120(2+√3)см²
проводим касательную, проводим радиусы в точки касания, и соединяем центры. кроме того, из центра меньшей окружности проводим пепендикуляр к радиусу большей окружности, проведенном у точку касания. этот перпендикуляр равен общей касательной (там прямоугольник: получился прямоугольный треугольник со сторонами d = корень(80) - линия центров, это гипотенуза треугольника, (r - r), и второй катет в качестве искомого расстояния.
x^2 = d^2 - (r - r)^2;
по условию r - r = 4; x^2 = 80 - 16 = 64; x = 8;