Объяснение:
1. Синус - это отношение противолежащего катета к гипотенузе, значит
16 : 40 = 0,4
2. Диагонали ромба являются биссектрисами его углов, пересекаются под прямым углом и точкой персечения делятся пополам.
Диагонали ромба делят его на 4 прямоугольных треугольника с катетами 9 и 3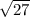
. Найдём острые углы этих треугольников, используя определение тангенса острого угла прямоугольного треугольника ( отношение противолежащего катета к прилежащему)
Пусть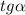 
= 
= 
= 
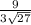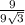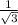,значит угол 
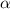= 30°, а значит второй острый угол будет равен 60°. Соответственно углы ромба будут 60° и 120°.
См. Объяснение
Объяснение:
∠В треугольника АВС равен ∠АСD треугольника ACD - согласно условию (отмечены одинаковыми дужками);
∠ВСА треугольника АВС равен ∠САD треугольника ACD - так как, согласно условию, ADCD является трапецией, поэтому AD║ BC, и угол
∠ВСА = ∠САD как углы внутренние накрест лежащие при параллельных прямых AD║ BC и секущей АС.
Согласно первому признаку подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Что и требовалось доказать.
СК⊥АВ; ΔВСК- прямокутний. СК=12-2=10 см. ВК²=ВС²-СК²=144-100=44;
ВК=√44=2√11 ≈6,63 см.
ΔАСК- прямокутний.АК²=АС²-СК²=324-100=224; АК=√224≈15 см.
АВ=ВК+АК=3,63+15=18,63 см
S=0,5(12+18,63)·10=153,15 см²≈153 см