1. 1) ∠AOD=∠BOC=130° (вертикальные), значит ∪ ВС=130°(стягивает центральный угол).
2)∪ АВ=∪АС- ∪ВС=180°-130°=50°, значит
∠АСВ =50/2=25 °(вписанный не центральный угол)
2. 1) ∆ АВС- равнобедренный , значит ∠ А=∠С=(180°-177°)/2=1,5°.
2) ∪ ВС=1,5°·2=3° (стягивает вписанный угол), тогда ∠ВОС=3° (центральный угол )
3. 1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания,
значит ∠ ОКМ=90°-7°=83° .
2) ∆ ОКМ- равнобедренный (ОК=КМ=r) , значит ∠ОКМ=∠ОМK=83°.
4. 1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания,
значит ∠ ОКМ=90°-84°=6°
2) ∆ ОКМ- равнобедренный (ОК=КМ=r) , значит ∠ОКМ=∠ОМK=6°.
5. ∠ ABC =90°(вписанный), т.к ∪ АС=180° (опирается на диаметр АС). Тогда ∠С=180°-90°-75°=25°
6. 1) ∪ AN=73°·2=146° (стягивает вписанный ∠ NBA). Тогда
∪ NB =∪ AB-∪AN=180°-146°=34°.
2) ∠NMB=34°/2=17° (вписанный не центральный угол)
7. 1) ∆ АОВ- равнобедренный(АО=ОВ=r), значит ∠ОАВ=∠АВО=15°. Тогда ∠ОВС =56°-15°=41°.
2) ∆ ВОС- равнобедренный(ВО=ОС=r), значит ∠ОВС=∠ВСО=41°.
8. ∆ АОВ =∆ СОD (AO=OD=r, CO=OB=r, ∠AОВ =∠CОD-вертикальные ), значит ∠ОАВ =∠ОСD=25°

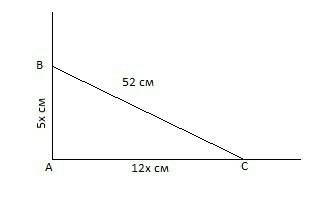
Построим прямой угол А и две материальные точки (В и С) которые движутся от тоски А со скоростью 5 см/с и 12 см/с. Расстояние между этими точками (ВС) будет являться гипотенузой треугольника АВС
Пусть время за которое между данными точками окажется расстояние равное 52 см будет равно х секунд, тогда пройденный путь (катеты АВ и ВС) 5х см и 12х см.
По теореме Пифагора: а^2+b^2=c^2 (где a и d катеты, c гипотенуза прямоугольного треугольника).
Подставим наши значения и решим полученное уравнение:
(5x)^2+(12x)^2=52^2
25x^2+144x^2= 2704
169x^2= 2704
x^2= 2704/169
x^2=16
x=√16
x1=-4
x2=4
Так как время не может быть отрицательным первый корень нам не подходит
ответ: через 4 секунды расстояние между точками будет равно 52 см.
30°
Объяснение:
∠ВDА = 180° - 150° = 30°
Раз треугольник равнобедренный, то углы при основании равны:
∠BDА = ∠ ВАD = 30°