Обозначим параллелограмм буквами ABCD. Пусть диагональ BD образует углы:
угол DBA=30 градусов, угол DB=90 градусов
Обозначим сторону AB=a, сторону BC=b. Так как у параллелограмма противолежащие стороны равны, то AB=CD=a, BC=AD=b
По условию задачи периметр параллелограмма равен:
P=AB+BC+CD+AD=a+b+a+b=2(a+b)=36
a+b=18
Рассмотрим треугольник ABD. Он прямоугольный, угол BDA=90 градусов
Выразим сторону AD:
AD=AB*sinABD=a*sin30=a/2
Значит, b=a/2
Подставим b вместо a:
a+b=36
a+a/2=18
3a/2=18
a=12
b=6
ответ: стороны параллелограмма равны 6см и 12см.
т.к треугольник равнобедренный, то высота это и медиана и биссектриса. следовательно получим два равных прямоугольных треугольника. углы в них 90 30 и 60 градусов
(углы при основании большого треугольника равны так как это равнобедренный треугольник и равны соответственно 180 - 120=60\2=30)
свойство прямоугольных треугольников, что катет лежащий против угла в 30 градусов равен половине гипотенузы
следовательно гипотенуза равна 23*2=46 см
по теореме пифагора находим основание маленького треугольника это 46^=23^2 +x^2
х= 23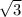
основание большого треугольника 23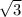
*2 = 46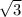
Объяснение: