120см²; 13см
Объяснение:
S=d1*d2/2=10*24/2=120cm²
За теоремой Пифагора:
С треугольника АВО(уголО=90°):
АВ²=ВО²+АО²=5²+12²=25+144=169; АВ=13см
("+" потому, что мы находили гипотенузу, а если бы надо было найти катет то "-")
1) Даны точки М(3; 5) и N(-6; -1).
Угловой коэффициент к прямой, проходящей через эти точки равен:
к = Δу/Δх = (-1-5)/(-6-3) = -6/-9 = 2/3.
Уравнение прямой будет у = (2/3)х + в.
Для определения величины в подставим в это уравнение координаты одной из точек, возьмём А.
5 = (2/3)*3 + в, отсюда в = 5 - 2 = 3.
ответ: уравнение у = (2/3)х + 3.
В общем виде 2х - 3у + 9 = 0 (после приведения к общему знаменателю).
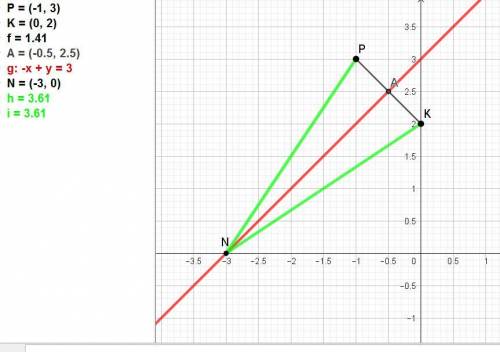
2) Пусть точка N, лежащая на оси абсцисс
и равноудаленная от точек Р(-1; 3) и К(0; 2), имеет координаты N(x; 0).
Используем равенство расстояний точки N от P и K.
NP² = (-1 - x)² + (3 - 0)² = 1 + 2x + x² + 9 = 10 + 2x + x².
NK² = (0 - x)² + (2 - 0)² = x² + 4.
Приравняем 10 + 2x + x² = x² + 4,
2x = 4 - 10
x = -6/2 = -3.
ответ: точка N(-3; 0).
К этому решению во вложении дан поясняющий рисунок.
Из него видно, что есть второй решения задания с использованием срединного перпендикуляра к отрезку АВ.
Решение.
1. Найдём площадь ромба.
Площадь ромба равняется половине произведения его диагоналей.
S= ½d¹d², где d¹ и d² — диагонали ромба, а S — его площадь.
S= ½×10×24= 12×10= 120 (см²).
2. Найдём сторону ромба.
У ромба все стороны равны, кроме того, диагонали ромба пересекаются под прямым углом.
В ΔВОС: угол ВОС =90°; ВО= ½ВD= 5 см; ОС= ½АС= 12 см.
По т. Пифагора:
ВС²= BO²+OC²;
BC²= 5²+12²;
BC²= 25+144;
BC²= 169;
BC= 13 см (-13 не удовлетворяет условие задачи). => сторона ромба равна 13 см.
ОТВЕТ: 120 см²; 13 см.
И там еще рисунок во вложении понять решение.