Это задание невыполнимо, так
как такого треугольника не су
ществует.
Объяснение:
Если боковая сторона 9см, то
основание равнобедренного
треугольника:
Р-2×9=38-18=20(см)
Длины сторон треугольника:
Основание - 20 см
1 боковая сторона - 9 см
2 боковая сторона - 9 см.
Треугольник скществует, если
сумма длин любых двух сто
рон треугольника больше
длины третьей стороны.
Проверим это условие:
1) 9+9=18 (см) сумма двух
боковых сторон;
18см<20см условие не выпол
няется.
Сумма длин двух боковых
сторон меньше длины осно
вания.
Отет:
Такой треугольник не сущест
вует.
В научной литературе зафиксировано не менее 400 доказательств теоремы Пифагора, что объясняется как фундаментальным значением для геометрии, так и элементарностью результата. Основные направления доказательств: алгебраическое использование соотношений элементов треугольника (таков, например, популярный метод подобия[⇨]), метод площадей[⇨], существуют также различные экзотические доказательства (например, с дифференциальных уравнений).
Через подобные треугольники
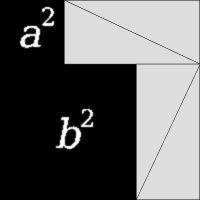
Одним из наиболее популярных в учебной литературе доказательств алгебраической формулировки является доказательство с использованием техники подобия треугольников, при этом оно почти непосредственно выводится из аксиом и не задействует понятие площади фигуры.[10] В нём для треугольника ABC с прямым углом при вершине C со сторонамиa,b,c, противолежащими вершинам A,B,C соответственно, проводится высота при этом согласно признаку подобия по равенству двух углов) возникают соотношения подобия: и , из чего непосредственно следуют соотношения.
При перемножении крайних членов пропорций выводятся равенства:
покомпонентное сложение которых даёт требуемый результат.
(хз надеюсь правильно)
Найдем центр вневписанной окружности KCM.
Угол между биссектрисами внешних углов при K и M равен 90 -С/2 =45.
Отрезок KM виден из центра под углом 45.
Центр лежит на биссектрисе угла С.
Точка A является искомым центром т.к. удовлетворяет обоим условиям.
В, D - точки касания на продолжениях сторон (радиусы в эти точки перпендикулярны касательным).
Точка касания вневписанной окружности со стороной треугольника (N) делит периметр пополам.
(Отрезки касательных из одной точки равны: CB=CD, KB=KN, MN=MD => CK+KN=CM+MN)
CB =CK+KN =(3+4+5)/2 =6