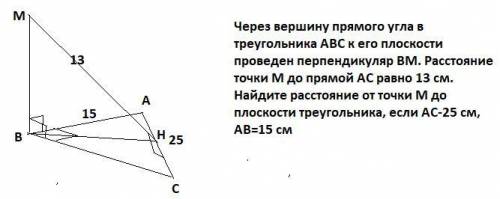
Через вершину прямого угла в треугольника АВС к его плоскости проведен перпендикуляр BM. Расстояние точки М до прямой АС равно 13 см. Найдите расстояние от точки М до плоскости треугольника, если АС-25 см, AB=15 см
Объяснение:
1)Расстоянием от точки до плоскости есть длина перпендикуляра к плоскости -отрезок ВМ .
Расстоянием от точки до прямой является перпендикуляр от точки до прямой. Пусть MH⊥AC , тогда ВН⊥АС по т. о трех перпендикулярах.
2) ΔВМН-прямоугольный , по т. Пифагора , ВМ=√(МН²-ВН²) . Необходимо найти ВН.
3) Найдем предварительно АН (*) : ВА²=АН*АС ⇒ 225=АН*25 ,
АН=9 см
3)ΔВАН -прямоугольный ВН=√(15²-9²)=12( см)
4) ВМ=√(13²-12²)=5 ( см)
===========================
(*)Свойства катетов прямоугольного треугольника: Квадрат катета равен произведению его проекции на гипотенузу.
Пусть окружность касается стороны CD в точке К, ОЕ1 и ОЕ2 - высоты трапеции АОQD
a) по условию АВ-диаметр окружности, значит АО=ОВ=R
ABCD - равнобедренная трапеция, следовательно ∠ВАD=∠CDA и AB=CD=2R
Если Q - середина CD, то ОQ - средняя линия трапеции. Следовательно AO=OB=CQ=QD=R
Также АО=ОН=R, то есть ΔАОН-равнобедренный, значит
∠ВАD=∠OHA
При этом ∠ВАD=∠CDA, следовательно ∠OHA=∠CDA, значит эти углы соответственные при параллельных прямых ОН и DQ и секущей АD.
Итак, ОН=QD и ОН || QD, следовательно DQOH-параллелограмм.
б) ∠ВАD=∠OHA=60°
∠АОН=180°-(∠ВАD+∠OHA)=180°-(60°+60°)=60° - ΔАОН - равносторонний, следовательно АН=R
∠ABC=∠BCD=180°-60°=120°
Если окружность касается CD, то ∠OKC=90° и ОК=R
Сумма всех углов в четырехугольнике равна 360°
∠ВОК=360°-(∠ОВС+∠OKC+∠DCK)=360°-(120°+90°+120°)=30°
Если ОQ -средняя линия трапеции, то OQ || AD, следовательно
∠BAD=∠BOQ=60°
∠KOQ=∠BOQ-∠ВОК=60°-30°=30°
ΔOQK -прямоугольный с прямым углом OKQ
OQ=HD- так как DQOH-параллелограмм
средняя линия трапеции =(а+в)/2