ответ: 32√3см²
Объяснение: обозначим вершины ромба А В С Д с диагоналями АС и ВД а точку их пересечения О. Противоположные углы ромба равны, а также диагонали ромба пересекаясь делятся пополам, образуя 4 равных прямоугольных треугольника, кроме того они делят углы из которых они проведены пополам, поэтому
<АВО=<СВО=АДО=СДО=60÷2=30°
ВО=ДО=8√3/2=4√3см. Найдём половину диагонали АС через тангенс угла в ∆АВО. Тангенс- это отношение противолежащего от угла катета к прилежащему, поэтому tgABO=AO/BO, тогда АО=СО=ВО×tg30°==4√3×√3/3=4×3/3=4см
Итак: АО=СО=4см, тогда АС=4×2=8см
Теперь найдём площадь ромба зная его диагонали по формуле:
S=½×d1×d2=½×8×8√3=32√3см²
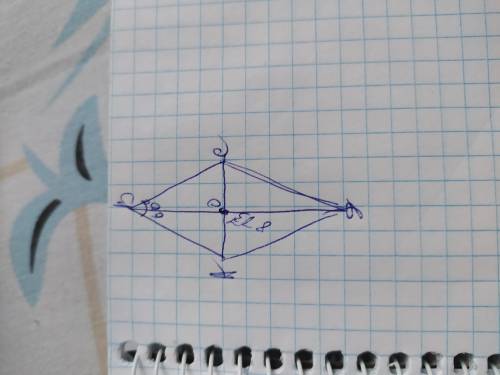
рисунок1
треугольник АВС равнобедренный с основанием АС, поэтому углы при основании А и С равны по 20°. угол В равен 180°-2*20°=140°, высота ВD является и биссектрисой угла В, поэтому углы АВD и СВDравны по 140°/2=70°, при вершине D
углы прямые.
рисунок 2
угол. внешний угол АDВ равен сумме двух внешних. с ним не смежных ,т.е. 90°+15°=105°. Углы при вершине В равны, т.к. ВD - биссектриса, они равны по 15°, угол при вершине А равен 75°-15°=60°, ∠С=90°
Рисунок 3
Т.к. высота ВD и медиана, то углы А и С равны по 45°, как углы при основании равнобедренного треугольника АВС, а угол АВС равен 45°, т.к. ВD еще и биссектриса угла В