1-случай ( точка М находится правее точки N);
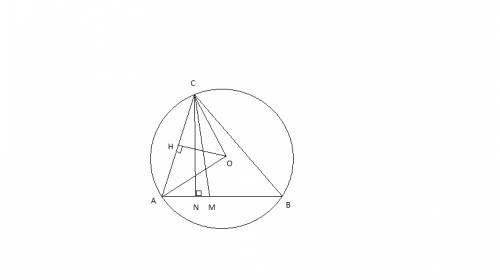
I. Построение:
Проведем r (радиусы) OC и ОА.
Проводим высоты ОН и СN.
II. Расчет:
1) Находим СN и ВN.
ΔОHС ≈ ΔBNC по 2-ум углам (∢СОН =∢СВА, т.к вписанный ∢СВА и центральный ∢СОА опираются на дугу АС, т.е. ∢СВА в 2 раза < ∢СОА, а ∢СОН = 1/2 ∢СОА, т.к. высота в равнобедренном треугольнике является и медианой и биссектрисой; ∢ОНС = ∢ВNС);
ΔOНC: ОС = 32,5; НС = 26; ОН = 19,5.
ΔВNС: СВ = 60; СN = ?; ВN = ?.
ОС/СВ = НС/СN = ОН/ВN; 32,5/60 = 26/СN = 19,5/ВN; СN = 48, ВN = 36.
2) Найдем NМ.
NМ = 14.
3) Найдем S ΔВМС.
S ΔCNB = 1/2 · 36 · 48 = 864.
S ΔCNM = 1/2 · 14 · 48 = 336.
S ΔCMB = 864 - 336 =528.
2-случай - по аналогии. Только точка М находится левее точки N.
Вложения
ответ: 3) 12.
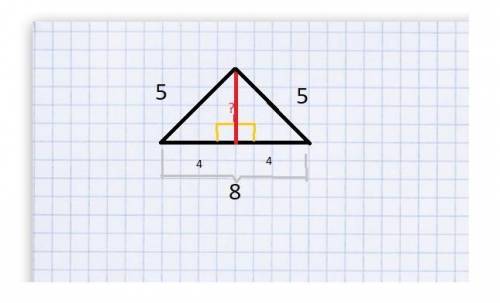
Итак, у нас есть равнобедренный треугольник со сторонами 5, 5, 8. И нужно найти его площадь. Например, по формуле:
S = (1/2)ah, где а - основание, а h - высота.
Но высоту мы не знаем. Попробуем ее найти. В предлагающемся ниже рисунке видно, что можно разделить этот треугольник на два прямоугольных одинаковых треугольника, у каждого из которых основание по 8/2 = 4, а гипотенуза - 5. Поэтому общая высота, по теореме Пифагора (сумма квадратов равна квадрату гипотенузы), равна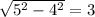 
. Теперь, когда мы знаем и высоту, и основание, мы сможем найти площадь:
S = (1/2)*3*8 = 12.
Следовательно, площадь данного треугольника равна 12 (номер ответа - 3).
MN=5,5 смс
Объяснение:
Так как N=90°, то MKN - прямоугольный треугольник
∠N=90°-60°=30°. Следовательно MN=½MK, MN=½11= 5,5 смс