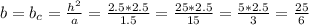6 ед.
Объяснение:
Пусть х будет одна сторона, тогда другая сторона будет (х+2).
Площадь это произведение длины на ширину.
Составляем уравнение.
х(х+2)=24
х²+2х-24=0
а=1
b=2
c=-24
D=b²-4ac=2²-4*1*(-24)=4+96=100
X1=(-b+√D)/2a=(-2+√100)/2*1=(-2+10)/2=4 ед. сторона прямоугольника.
Х2=(-b-√D)/2a=(-2-10)/2=-12/2=-6 число отрицательное не подходит.
Одна сторона х=4. Другая х+2. Подставим значение х.
4+2=6 ед. другая сторона прямоугольника.
ответ:6 большая сторона прямоугольника.
Проверка
6*4=24 ед² площадь прямоугольника.
Расчет характеристик
Площадь сечения
F = F1 - F2 - F3;
где F1 - площадь прямоугольника 1;
F2 - площадь прямоугольника 2;
F3 - площадь круга 3.
F1 = h1 x b1 = 45 x 60 = 2700 мм²;
F2 = h2 x b2 = 15 x 45 = 675 мм²;
F3 = PI x R32 = PI x 7,5² = 176.715 мм²;
F = 2700 - 675 - 176.715 = 1848.285 мм².
Cтатические моменты
Обозначим начало координат в самой левой нижней точке сечения.
Тогда статический момент сложной фигуры относительно оси Х равен сумме статических моментов простых фигур составляющих эту фигуру.
Sx = Sx1 - Sx2 - Sx3;
где Sx1 - статический момент прямоугольника 1;
Sx2 - статический момент прямоугольника 2;
Sx3 - статический момент круга 3.
Sx1 = F1 x Xc1 = 2700 x 30 = 81000 мм³;
Sx2 = F2 x Xc2 = 675 x 11.25 = 15187.5 мм³;
Sx3 = F3 x Xc3 = 176.715 x 29.9 = 3976.0782 мм³;
Sx = 81000 - 15187.5 - 3976.0782 = 61836.422 мм³.
Cтатический момент сложной фигуры относительно оси Y равен сумме статических моментов простых фигур составляющих эту фигуру.
Sy = Sy1 - Sy2 - Sy3;
где Sy1 - статический момент прямоугольника 1;
Sy2 - статический момент прямоугольника 2;
Sy3 - статический момент круга 3.
Sy1 = F1 x Yc1 = 2700 x 22.5 = 60750 мм³;
Sy2 = F2 x Yc2 = 675 x 7.5 = 5062.5 мм³;
Sy3 = F3 x Yc3 = 176.715 x 30 = 5301.4376 мм³;
Sy = 60750 – 5062.5 - 5301.4376 = 50386.062 мм³.
Центр тяжести
Зная площадь сечения и его статические моменты можно определить координаты центра тяжести по следующим формулам:
Xc=Sx/F, Yc=Sy/F
Xc = 61836.422 : 1848.285 = 33,4561 мм;
Yc = 50386.062 : 1848.285 = 27,260975 мм.
Значения координат получены относительно выбранного начала координат O.
ответ: 3)
Объяснение:
известно: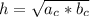
в данной задаче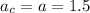
и найти нужно b: