1) В четырехугольнике ABCD точки E и F — соответственно середины равных сторон AB и CD . Серединные перпендикуляр к стороне AD пересекает серединный перпендикуляр к стороне BC в точке P . Докажите, что серединный перпендикуляр, проведенный к отрезку EF проходит через точку P .
2) В четырехугольнике ABCD серединные перпендикуляры к сторонамAB и CD пересекаются на стороне AD . Известно, что \angle A = \angle D . Докажите, что в четырехугольнике диагонали равны.
3) В квадрате ABCD даны точки E и F соответственно на сторонах AB и BC ,причем \angle AED = \angle FED . Докажите равенство EF = AE + FC
так???!!!

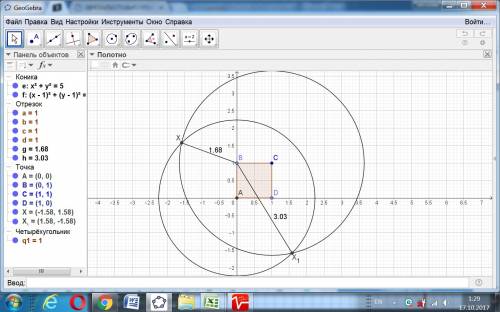
ответ:10 см
Объяснение:
Проведём АД⊥ВС, тогда (ВС*АД):2=S ΔАВС,
(12*АД) : 2=30;
12*АД=30*2;
12*АД=60;
АД=60:12;
АД=5.
ΔАВД: ∠АДВ=90°, sin∠В=АД:АВ ⇒АВ=АД:sin30°=5: 1/2=10 (см)