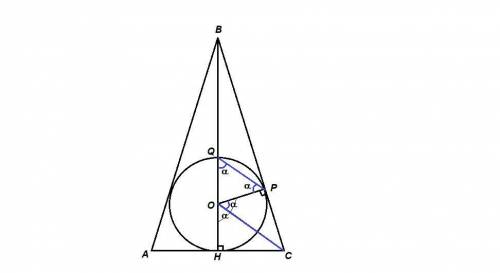
ВН - биссектриса равнобедренного треугольника, проведенная к основанию, значит ВН - высота.
ОР⊥ВС как радиус, проведенный в точку касания.
ΔOPQ равнобедренный (OP = OQ как радиусы), значит
∠OPQ = ∠OQP = α
∠POH = ∠OPQ + ∠OQP = 2α как внешний угол треугольника OPQ.
ΔСОН = ΔСОР по катету и гипотенузе (∠СНО = ∠СРО = 90°, ОН = ОР как радиусы, ОС - общая), значит
∠СОР = ∠СОН = 1/2 ∠РОН = α.
Итак, ∠OPQ = ∠COP = α, а эти углы - внутренние накрест лежащие при пересечении прямых QP и ОС секущей ОР, значит
QP ║ OC.
Объяснение:
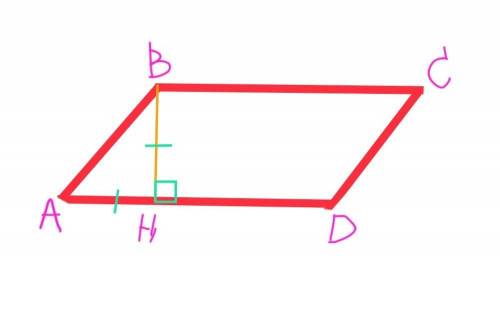
ВН – высота, проведённая к стороне АD, по условию, тогда угол ВНА=90°.
Так как ∆АНВ по условию, равнобедренный, то найдем угол ВАН.
Углы при основании в равнобедренном треугольнике равны, тогда:
Угол ВАН = (180°– угол ВНА)÷2=(180°–90°)÷2=45°.
В параллелограмме, углы при одной его стороне в сумме дают 180°, тогда:
Угол АВС=180°– угол ВАD= 180°–45°=135°
Противоположные углы в параллелограмме равны, тогда:
Угол BCD= угол BAD=45°
Угол ADC= угол АВС=135°
ответ: Угол BCD=45°; угол BAD=45°; угол ADC=135°; угол АВС=135°
ответ: 64√3/9
так как пирамида правильная, то в основании квадрат, площадь которого 4^2=16
дальше смотри фото