Колон отличался от раба тем,что он имел свободу и мог арендовать землю,владел имуществом,мог жениться,а раб был собственностью своего господина который кормил его и не дал бы умереть с голода.
Поэтому конечно лучше работал колон учитывая что он работает на себя.
P.s Колоны свободны, а рабы нет
P.s Колонов стали закреплять за участками земли, они не могли уходить с них, дети колонов должны были оставаться в том месте, где родились их родители. Такое же положение было у «рабов с хижинами», которые не могли покинуть участок, но их можно было продать вместе с землей.
Объяснение:
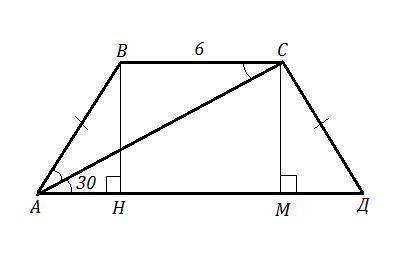
АВСД - равнобокая трапеция, АВ=СД, ВС=6 см, ∠АВС=120° , ∠САД=30°. Найти АС.
Так как ∠АВС=120°, то ∠ВАД=180°-120°=60° ,
∠САД=30° ⇒ ∠ВАС=∠ВАД-∠САД=60°-30°=30° .
Значит диагональ АС - биссектриса ∠А .
∠АСВ=∠САД=30° как внутренние накрест лежащие при АД || ВC и секущей АС ⇒ ΔАВС - равнобедренный , т.к. ∠ВАС=∠АСВ .
Значит, АВ=АС=6 см .
Опустим перпендикуляры на основание АД из вершин В и С: ВН⊥АС , СМ⊥АД , получим прямоугольник ВСМН и два треугольника АВН и СМД .
Рассмотрим ΔАВН: ∠ВНА=90°, ∠ВАН=∠ВАД=60° , АВ=6 см ⇒
∠АВН=90°-80°=30°
Против угла в 30° лежит катет, равный половине гипотенузы ⇒ АН=6:2=3 см.
Так как ΔАВН=ΔСМД (по гипотенузе АВ=СД и острому углу ∠ВАД=∠АДС), то МД=АН=3 см.
НМ=ВС=6 см как противоположные стороны прямоугольника ВСМН.
АД=АН+НМ+МД=3+6+3=12 см.
Сторона шестиугольника равна 24√3/6=4√3
Вписываем треугольник чтобы его вершины совпадали с вершинами шестиугольника через одну. В результате имеем ещё три треугольника с двумя сторонами шестиугольника и одной вписанного в круг треугольника. Рассмотрим один из них. Проведём из вершины такого треугольника перпендикуляр к основанию. Тогда он разделит этот треугольник на два прямоугольных треугольника. Катет одного из них будет равен половине стороны вписанного искомого треугольника. Находим угол между катетом и гипотенузой
α=120/2=60 -половина угла шестиугольника
Катет равен 4√3*sin60=4√3*(√3/2)=6
Тогда сторона треугольника равна 6*2=12
Объяснение: