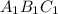- его проекция на плоскость P. 
.
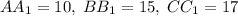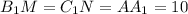дм. Тогда BM = 15-10 = 5 дм, CM = 17-10 = 10 дм.
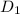. Этот перпендикуляр разделит отрезок NM пополам. Значит 
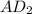медиана треугольника 
.
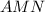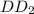- средняя линия трапеции BCNM. Его длина 
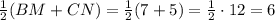дм.
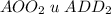подобны по первому признаку: 
- общий, 
.
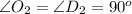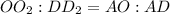
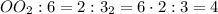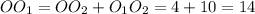дм.
дм.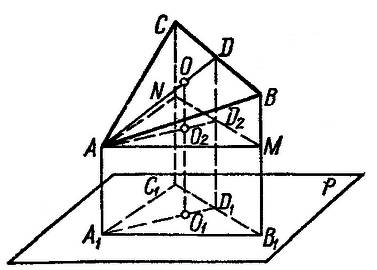
Объяснение:
ΔАВС равнобедренный ,значит ∠С=∠ВАС=80.
∠КАР=80-40=40.
ΔАКР-равнобедренный ,значит ∠КАР=∠КРА=40.Найдем ∠АКР=180-40-40=100
КР║АС, тк. сумма односторонних углов 180 :∠АКР+∠КАС=100+80=180 при секущей АК.