Понятно, что точка С является одной из вершин при основании равнобедренного треугольника ΔABC (иначе бы она могла располагаться где угодно, а периметр треугольника мог бы быть сколь угодно большим или сколь угодно маленьким). Тогда нам нужно достроить ее симметрично точке А или симметрично точке B. Пусть A - верхняя вершина равнобедренного треугольника ΔABC, а вершины B и C - это его вершины при основании. Тогда требуется построить точку С симметрично точке B относительно высоты (ну или по совместительству биссектрисы и медианы) из вершины A в треугольнике ΔABC. Тогда пусть ее координаты по осям y, z будут такими же, как у B, тогда координата по оси x будет равна 8 - 5 = 2, ведь 5 есть среднее арифметическое чисел 2 и 8 (здесь 5 - абсцисса точки A, потому то относительно ее и считаем). Тогда BC = 8 - 2 = 6. Также имеем точку С(2; -3; 3). Возьмем точку K - точку, в которую падает высота (медиана и биссектриса) из вершины А. Ее координаты, очевидно, равны (5; -3; 3). Спроецируем полученный треугольник на плоскость Oxy, где получим некий ΔMLN. Несложно посчитать его стороны. ML = √((Ax-Cx)²+(Ay-Cy)²)=√(3²+2²)=√13. Аналогично MN = √13. LN = BC = 6 (очевидно). Опустим перпендекуляры BW и CW к AM, тогда, исходя из параллельности прямых WB = MN = WC = ML = √13. Заметим, что AW = Az - Cz = Az - Bz = 4 - 3 = 1. По теореме Пифагора AC = AB = √(1² + (√13)²) = √14. Тогда PΔabc = 6 + √14 + √14 = 6+2√14 = 2*(3+√14).
ответ: PΔabc = 2*(3+√14).
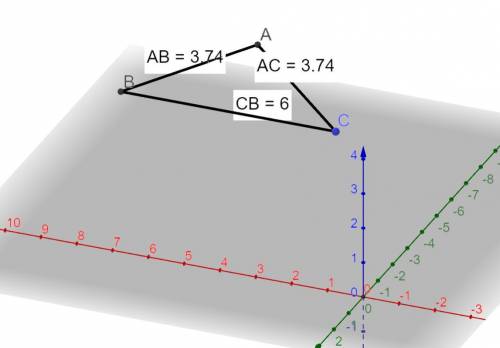
Длина АВ=√(2-1)²+(3-6)²=√10
Длина ВС=АВ=√10 ( т.к квадрат)
Координата "y" точки С такая же как и у вершины В ( на рисунок глянь)
Найдем координату х точки С:
ВС=√(х₂-х₁)²+(y₂-y₁)²
х₂; y₂- координата вершины С
х₁; y₁- координата вершины В
√10=√(х₂-2)²+(3-3)²
10=х₂-2⇒х₂=12
Координаты точки С (12;3)
Находим длину (модуль) вектора АС:
Координаты точки С (12;3)
Координаты точки А (1;6)
АС=√(х₂-х₁)²+(y₂-y₁)²
х₂; y₂- координата вершины С
х₁; y₁- координата вершины A
АС=√(х₂-х₁)²+(y₂-y₁)²=√(12-1)²+(3-6)²=√130
Координаты вектора АС:
АС ((х₂-х₁);(y₂-y₁))
АС(11;-3)