Поскольку высоты равны,то этот треугольник равнобедренный=> C1AC=A1CA
Возьмем треугольники АСС1 и AA1C,докажем,что они равны:
1) AA1=C1C
2)AC общий
3)угол AC1C=AA1C
Поскольку высоты равны,то этот треугольник равнобедренный=> C1AC=A1CA
От первого признака равенства треугольников получаем,что эти треугольники равны:
если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
BA1=A1C=> AA1 является медианой треугольника,АА1=C1C=> C1C тоже является медианой.
Если у треугольника и медианы,и высоты совподают,то этот треугольник является равносторонным.=>ответ /_B=60°
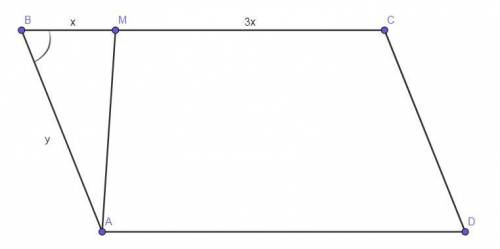
На стороне ВС параллелограмма ABCD отмечена такая точка М, что ВМ : МС = 1 : 3. Чему равна площадь треугольника АВМ, если площадь параллелограмма равна S?
Чертёж смотрите во вложении.
Дано:
Четырёхугольник ABCD - параллелограмм.
Точка М ∈ ВС.
ВМ : МС = 1 : 3.
S(ABCD) - S.
Найти:
S(ΔАВМ) = ?
Пусть ВМ = х, тогда МС = 3х, АВ = у. Площадь ΔАВМ обозначим как S₁.
Площадь параллелограмма равна произведению смежных сторон и синусу угла между ними.
Следовательно -
S(ABCD) = ВС*АВ*sin (∠В)
ВС = ВМ+МС = х+3х = 4х.
То есть -
S = 4ху*sin (∠В)
Рассмотрим ΔАВМ.
Площадь треугольника равна половине произведения смежных сторон и синуса угла меду ними.
То есть -
S(ΔАВМ) = 0,5*ВМ*АВ*sin (∠В)
S₁ = 0,5*хy*sin (∠В).
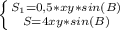
Из первого уравнения системы следует, что -
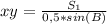
Подставим это значения во второе уравнение системы -
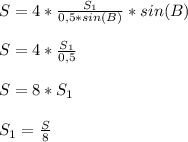
S(ΔАВМ) = S(ABCD)/8
S(ΔАВМ) = S/8.
ответ: S/8.
Объяснение:
ЗАДАНИЕ 2
а₂=101,а₄=102
По свойству "каждый член арифметической прогрессии, начиная со второго, есть среднее арифметическое предыдущего и последующего членов"
получем а₃=(а₂+а₄)/2 ,а₃=(101+102)/2=101,5
d=101,5-101=1,5
а₁=а₂-d=101-1,5=99,5
аₙ=а₁+d(n-1), а₉= 99,5+8*1,5= 111,5
ЗАДАНИЕ 4
а₃=49 ,а₆=58 . Наити а₂₀
ПРименим аₙ=а₁+d(n-1), и вычтем из второго уравнения первое
49=а₁+2d
58=а₁+5d
⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻⁻
9=3d, значит d=3. Найдем а₁, 49=а₁+2*3 ,а₁=43.
Найдем а₂₀=а₁+d(20-1), а₂₀=43+3*19=100
ЗАДАНИЕ 6
а₅=1 ,а₆=-4 . Наити а₁₃
d=а₆-а₅=-4-1=-5
ПРименим аₙ=а₁+d(n-1) для а₅=1 : 1=а₁+4*(-5) ,а₁=1+20=21
Найдем а₁₃=а₁+d(13-1), а₁₃=21+(-5)*12=21-60=-39