Ромб - это параллелограмм, у которого все стороны равны.
Ромб имеет 2 диагонали. Каждая из диагоналей ромба делит его на 2 симметричных треугольника, поэтому, диагонали являются осями симметрии ромба.
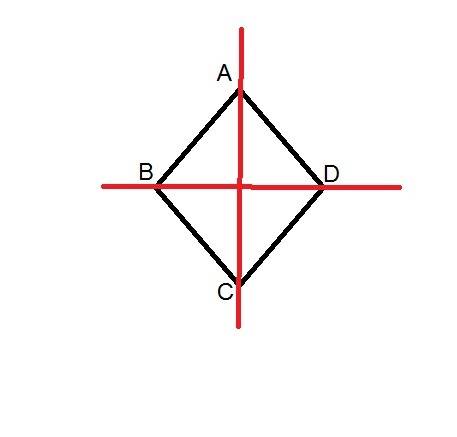
На рисунке изображен ромб ABCD, с диагоналями АС и ВD.
AC и BD - оси симметрии ромба ABCD, поэтому нельзя построить фигуру, симметричную ромбу ABCD, относительно прямой BD.
Прямая BD - одна из осей симметрии, и ромб симметричен сам себе, относительно своей оси симметрии.
Наличие оси симметрии, характеризует ромб, как симметричную фигуру. то есть, фигуру, состоящую из отраженно равных частей, относительно прямой на плоскости.
в нашем случае, прямая AD, делит ромб на 2 отраженно равных треугольника (симметричных треугольника) ABD и CDB.
Рисунок во вложении
Рассмотрим прямоугольную трамецию АВСD, в прямоугольных трапециях всегда 2 угла равны 90 градусам (по свойству прямоугольной трапеции), то есть угол А и угол В равны, а они равны 90 градусам. Следовательно, если нам дано, что угол D равен 20 градусов, а все углы кроме одного нам известны, то мы можем найти угол С. Сумма углов любой трапеции равна 360 градусам (по свойству трапеции), следовательно, угол С равен 360-90-90-20=160 градусов
ответ: угол А - 90 градусов, угол В - 90 градусов, угол С - 160 градусов, угол D - 20 градусов
Сумма внешних углов любого выпуклого многоугольника равна 360°.
Так как по условию сумма внешних углов правильного многоугольника в 3,5 раза меньше суммы его внутренних углов, то сумма внутренних углов равна
360°·3,5 = 1260°
Сумма внутренних углов выпуклого многоугольника вычисляется по формуле:
180°(n – 2), где n – количество углов многоугольника.
тогда 180°(n –2) = 1260°
n – 2 = 1260°:180°
n = 7 + 2
n = 9
Следовательно, в данном многоугольнике 9 углов, тогда и 9 сторон. В правильном многоугольнике все стороны равны. Для нахождения длины одной стороны периметр разделим на 9:
а = Р : 9 = 144 : 9 = 16
ответ: длина стороны 16 см.