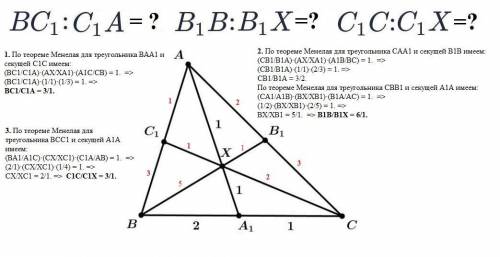
ВС1/С1А = 3/1. В1В/В1Х = 6/1. С1С/С1Х = 3/1.
Объяснение:
1. По теореме Менелая для треугольника ВАА1 и секущей С1С имеем:
(ВС1/С1А)·(АХ/ХА1)·(А1С/СВ) = 1. =>
(ВС1/С1А)·(1/1)·(1/3) = 1. =>
ВС1/С1А = 3/1.
2. По теореме Менелая для треугольника САА1 и секущей В1В имеем:
(СВ1/В1А)·(АХ/ХА1)·(А1В/ВС) = 1. =>
(СВ1/В1А)·(1/1)·(2/3) = 1. =>
СВ1/В1А = 3/2.
По теореме Менелая для треугольника СВВ1 и секущей А1А имеем:
(СА1/А1В)·(ВХ/ХВ1)·(В1А/АС) = 1. =>
(1/2)·(ВХ/ХВ1)·(2/5) = 1. =>
ВХ/ХВ1 = 5/1. => В1В/В1Х = 6/1.
3. По теореме Менелая для треугольника ВСС1 и секущей А1А имеем:
(ВА1/А1С)·(СХ/ХС1)·(С1А/АВ) = 1. =>
(2/1)·(СХ/ХС1)·(1/4) = 1. =>
СХ/ХС1 = 2/1. => С1С/С1Х = 3/1.
меньшее основание трапеции равно 5 см
большее основание равно 45 см
площадь трапеции равна 375 см2.
Объяснение:
Высоты трапеции BF и CE равны диаметру вписанной окружности.
Прямоугольные треугольники ABF и DCE равны.
По теореме Пифагора из треугольника ECD находим ED:
ED2=CD2−CE2;ED2=252−152;ED=252−152−−−−−−−−√;ED=20 см.
Так как в трапецию вписана окружность, то суммы противоположных сторон трапеции равны.
BC+AD=AB+CD;BC=FE, пустьBC=x, тогдаx+20+x+20=25+25;x=5.
BC= 5 см, AD= 20+5+20 = 45 см.
Площадь трапеции S= BC+AD2⋅EC=5+452⋅15 = 375 см2.
Основания трапеции равны 5 см и 45 см, площадь трапеции равна 375 см2.
Октаэдр - правильный выпуклый многогранник, с 8 гранями, являющимися правильными треугольниками.
Таким образом площадь поверхности октаэдра равна 8 площадям боковых граней: .
.
Площадь грани: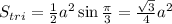 , где a - сторона треугольника (длина ребра).
, где a - сторона треугольника (длина ребра).