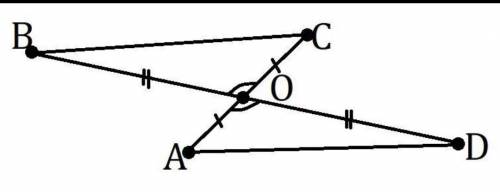
Рассмотрим треугольники BOC и DOA:
AO=0C и BO=OD- по условию;
<BOC = <DOA-как вертикальные;
треугольник ВОС = треугольнику DОА - по двум сторонам и углу между ними.
• В равных треугольниках углы, лежащие напротив равных сторон, равны.
<CBO лежит напротив ОС;
<ADO лежит напротив АО;
OC = AO следует <EBO = <ADO.
<CBO и <ADO - накрест лежащие углы при пересечении ВС и AD с секущей BD.
Раз <CBO=<ADO, то по признаку параллельности прямых получим, что вс|| AD. Что и требовалось доказать.
Объяснение:
1)
Сумма углов в треугольнике равна 180°
Пусть градусная мера угла <М будет 2х°; второго угла <N 4х°; третьего <P 3х°.
Составляем уравнение.
2х+4х+3х=180°
9х=180
х=180/9
х=20
2*20=40° угол <М
4*20=80° угол <N
3*20=60° угол <Р.
ответ: <М=40°; <N=80°; <P=60°
2)
<A+<B=160°; внешний угол равен сумме углов не смежных с ним.
Пусть градусная мера угла <А будет 2х°; <В будет 3х°.
Составляем уравнение
2х+3х=160°
5х=160
х=160/5
х=32
32*2=64° угол <А
32*3=96° угол <В
Сумма углов в треугольнике равна 180°
<ВСА=180°-<А-<В=180°-64°-96°=20°
ответ: <А=64°; <В=96°; <ВСА=20°
3)
<ВКО=180°, развернутый угол.
<ВКС=<ВКО-<СКО=180°-105°=75°
В равнобедренном треугольнике углы при основании равны.
<ВКС=<ВСК=75°
Сумма углов в треугольнике равна 180°
<В=180°-<ВКС-<ВСК=180°-75°-75°=30°
ответ: 75√3 ед²
Объяснение:
Дано: КМРТ - трапеция, КМ=РТ, ∠Т=60°, КР⊥РТ; КТ=20. Найти S(КМРТ).
Рассмотрим ΔКРТ - прямоугольный; ∠РКТ=90-60=30°, значит, РТ=0,5КТ=10 по свойству катета, лежащего против угла 30 градусов.
Проведем высоту РН и рассмотрим ΔРТН - прямоугольный;
∠ТРН=90-60=30°, значит, ТН=0,5РТ=5.
Найдем РН по теореме Пифагора:
РН²=РТ²-ТН²=100-25=75; РН=√75=5√3.
Найдем МР. ∠МРК=∠РКН=30° как внутренние накрест лежащие при МР║КТ и секущей КР; ∠МКР=60-30=30°, значит, ΔКМР - равнобедренный, МР=КМ=10.
S(КМРТ)=(МР+КТ)/2 * РН = (10+20)/2 * 5√3 = 15*(5√3)=75√3 ед²