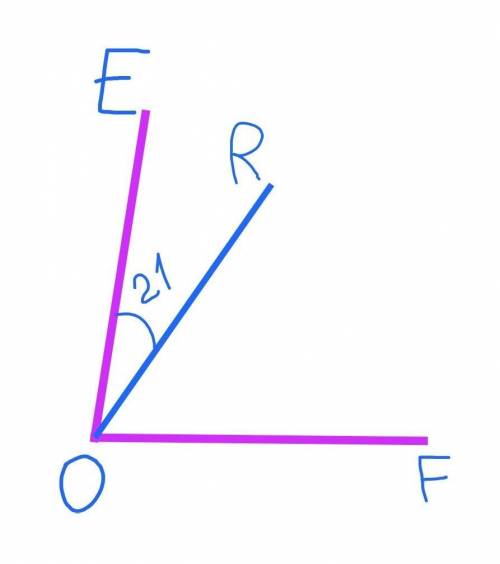
№1
Угол ЕОR=21° по условию
Угол ROF в 3 раза больше угла ЕОR, тогда угол ROF=21°*3=63°.
Угол ЕОF=угол EOR+угол ROF=21°+63°=84°
ответ: 84°
№2
Пусть длина ВС – х, тогда длина АС – 2х
АВ=АС+ВС;
15=2х+х
15=3х
х=5
Тогда длина ВС=5 см, а длина АС=2*5=10 см.
ответ: 10 см, 5 см
№3
а) Угол смежный углу КОЕ – это угол СОЕ (прямая СК и общая сторона ОЕ) или угол NOK (прямая NE и общая сторона ОК)
ответ: два варианта. Выбирай любой.
b) 1 пара: угол КОЕ и угол CON (пересекающиеся прямые СК и NE)
2 пара: угол СОЕ и угол KON (пересекающиеся прямые СК и NE)
c) Так как углы КОЕ и CON вертикальны, то они равны. Угол CON=46° по условию, тогда и угол КОЕ=46°.
d) Угол СОК – развернутый, тоесть он равен 180°;
Угол РОК=65° по условию;
Угол CON=46° по условию;
Угол PON=угол СОК–угол РОК–угол CON=180°–65°–46°=69°
ответ: 69°
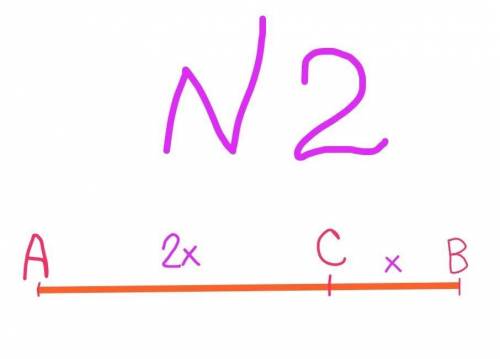
(МН·РН) = 4 ед.
(ОР·РК) = -2 ед.
Объяснение:
В прямоугольнике противоположные стороны равны =>
вектора МН = РК.
∠ РОК = 180° - 120° = 60° ( смежные углы).
В прямоугольнике диагонали равны и точкой пересечения делятся пополам =>
Треугольник РОК равносторонний, так как
ОК=ОР и ∠ РОК = 60°). => ОР = ОК = РК = 2 ед.
ОН=ОР = 2 ед. РН = 4 ед.
Скалярное произведение векторов можно записать так:
a·b=|a|·|b|c·сosα.
Определение: "Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором".
Совместим начала векторов ОР и РК в точке О. Тогда угол между векторами ОР и ОК' (вектора ОК и ОК' равны) равен 120°.
Векторное произведение указанных в условии векторов:
(МН·РН) = (РК·РН) = 2·4·Cos60° = 4 ед.
(ОР·РК) = 2·2·Cos120° = -2 ед.